Aerodynamika piłki nożnej a FloEFD
Rok 2018 przyniesie dużo zabawy miłośnikom piłki nożnej. Poza standardowymi krajowymi i międzynarodowymi rozgrywkami, będziemy również mogli cieszyć się zbliżającymi się mistrzostwami świata. Więcej drużyn oraz więcej meczy oznacza więcej minut gry, a zatem więcej szans na piękne gole. W rzeczy samej, kiedy najlepsi gracze na planecie zbierają się w tym samym miejscu i biorą udział w tym wydarzeniu sportowym, kolekcja pięknych goli jest pewna! Ale… dlaczego piszemy o tym na blogu GM System? Ponieważ chodzi o ważkie zagadnienie: aerodynamika piłki nożnej a FloEFD. Co może mieć wspólnego piłka nożna z systemem do obliczenia i symulacji? FloEFD bada opisywane zjawiska…
Oczywistym jest, że dla entuzjasty futbolu najlepsze gole to te strzelone przez jego reprezentację narodową, szczególnie, jeśli przesądzają o zwycięstwie w meczu lub nawet w samych mistrzostwach. Jednak każdy miłośnik piłki nożnej preferuje strzały ze średniego lub długiego dystansu, które zmieniają trajektorię lotu po długiej krzywej w powietrzu, często niepoprawnie nazywanej parabolą.
Umiejętność niezbędna do strzelenia takiego gola może być osiągnięta tylko przez nielicznych. Siła i podkręcenie podczas oddania strzału określą trajektorię lotu piłki, oszukując oczy widzów i bramkarza. Pokazana w zwolnionym tempie piłka przelatuje poza jego zasięgiem, docierając do celu i lądując w siatce.
Lecz dlaczego piłka skręca?
Aby odpowiedzieć na to pytanie musimy wyjaśnić aerodynamikę kuli, zakładając, że piłka jest mniej więcej sferyczna.
Aerodynamika kuli
Podczas lotu w kierunku bramki na piłkę działają dwie siły: grawitacja oraz aerodynamika. Rozróżniamy 3 rodzaje siły aerodynamicznej:
- Siła oporu: to siła wytwarzana przez powietrze przeciwnie do kierunku jej ruchu powodując zmniejszenie prędkości piłki.
- Efekt Magnusa: kiedy obracająca się piłka poruszając się względem płynu (powietrza), powoduje powstawanie siły prostopadłej do osi obrotu i trajektorii ruchu jednocześnie modyfikując jej ślad aerodynamiczny.
- Drganie: występuje kiedy oderwanie od warstwy przyściennej nie jest homogeniczne. Jakikolwiek brak równowagi w oderwaniu wywoła zaburzenie w polu oddziałującego ciśnienia, które generuje siłę boczną. Oderwanie występuje w części sferycznej piłki po stronie przeciwnej do kierunku ruchu. Dlatego też, zgromadzona siła będzie również prostopadła do trajektorii lecz niekoniecznie w tym samym kierunku co siła wywołana efektem Magnusa. W określonych warunkach jednak kierunki działania tych sił mogą być równoległe, a przeciwne zwroty spowodują ich redukcję. Rzadziej zdarza się, że siła wywołana oderwaniem może zmienić zwrot zgodny z kierunkiem ruchu. Zmiana taka spowoduje zmianę wypadkowej siły oporu piłki podczas ruchu (patrz link poniżej).
Występuje bardzo wysokie prawdopodobieństwo nieregularnego oderwania w warstwie przyściennej dla niepodkręcanych i/lub bardzo gładkich piłek. Wartość siły wywołana tym zjawiskiem nie jest bardzo duża, dlatego też, im niższy ciężar piłki tym bardziej wyolbrzymiony będzie wpływ. Zjawisko to powszechnie znane jest jako „efekt piłki plażowej”, występujące podczas usiłowania prostego kopnięcia plastikowej piłki plażowej. Jako że nie możemy przewidzieć oderwania, nastąpi ono przypadkowo, a generowana siła zmieni wartość oraz kierunek nagle, generując chaotyczną trajektorię, która jest zupełnie nieprzewidywalna.
Jednak, podczas gdy piłka plażowa jest dobra do zabawy na plaży, jej nieprzewidywalność podczas kopnięcia sprawia, że nie jest pożądana w profesjonalnych (a nawet amatorskich) meczach piłki nożnej. Możliwość przewidywania dokąd piłka zmierza, zmniejsza czynnik przypadkowości i uzależnia jej lot od umiejętności gracza. Umiejętność natomiast jest czymś, co można wytrenować.
Zmniejszanie drgań
Istnieją dwa sposoby na zmniejszenie drgań do minimum. Zwiększenie chropowatości powierzchni zwiększa grubość warstwy przyściennej, ułatwiając jej oderwanie. Dla grubszych warstw przyściennych oderwanie nastąpi przy niższych prędkościach. Jako że piłka podczas swojego ruchu zwalnia, nie jest to nagłe i nieregularne oderwanie, które może spowodować jej drganie. Większa szorstkość sprawia, że piłka jest bardziej stabilna dla szerszego zakresu prędkości, lecz również zwiększa opór tarcia. Zatem piłka również szybciej zwolni, osiągając krótszy dystans.
Drugi mechanizm jest podobny do chropowatości, lecz na znacznie większą skalę. Chropowatość jest sposobem na ilościowe określenie drobnych nieregularności na powierzchni. Jednakże, mogą one być większe. W piłce do piłki nożnej, nierównościami są niewielkie „rowki” powstałe w miejscach połączeń łat.
Nierówności mają różny wpływ na to, czy piłka obraca się czy nie. Jeżeli nie obraca się, działają one jako generatory wiru. Kiedy przepływ napotyka przeszkodę, bardziej prawdopodobne jest, że nastąpi oderwanie. Im większa przeszkoda, tym łatwiejsze oderwanie. Dlatego też w konstrukcji nierówności, piłki muszą być optymalnych rozmiarów. Również równomierny rozkład przeszkód doprowadzać będzie do bardziej homogenicznej strefy oderwania (a to zmniejsza drganie).
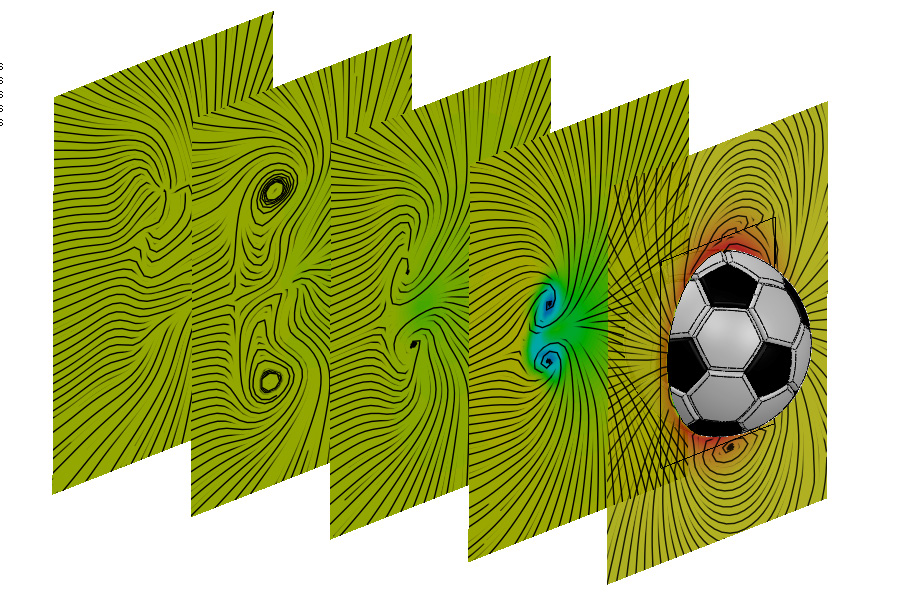
Jeżeli piłka obraca się, przeszkody mają inny wpływ na stronę, która porusza się razem z przepływem powietrza (lewa strona na obrazku) niż na stronę przeciwną (prawa strona na obrazku). Strona poruszająca się do przodu otrzymuje pomoc od przeszkody, więc jak gdyby pompuje powietrze. Z drugiej strony, przeszkoda zwrócona jest do wiatru w kierunku przeciwnym, generując wir i powodując oderwanie warstwy przyściennej.
Rys. 1. Linie prądów i kontury prędkości w widoku z góry. Powietrze napływa z lewej strony i piłka obraca się w kierunku przeciwnym do ruchu wskazówek zegara na osi prostopadłej do obrazu.
Rys. 2. Kilka sekcji pokazujących ewolucję turbulentnego przepływu powietrza, które jest załamywane, następnie piłka obraca się.
Rys. 3. Linie prądów pokazują, w jaki sposób przepływ jest załamywany przez obracającą się piłkę. Siła Magnusa działa w kierunku przeciwnym do załamania powietrza.
Rys. 4. Wektory I kontury prędkości w widoku z góry. Powietrze napływa z lewej strony i piłka obraca się w kierunku przeciwnym do ruchu wskazówek zegara w osi prostopadłej do obrazu.
Idealnie zaprojektowana piłka
Oczywiście wcześniejsze piłki nie były projektowane w oparciu o wszystkie te rozważania aerodynamiczne. Zaczęły być kuliste na tyle, na ile to możliwe i produkowane jak najlepiej. Złe projekty zostały odrzucone: zbyt ciężkie, zbyt nieprzewidywalne, dziwnie odbijające się, itd. Zatem nie jest zbiegiem okoliczności, że jednym z najlepszych projektów został niemal uniwersalny wzór sześciokątów i pięciokątów, łatwy w produkcji, o szwach prawidłowego rozmiaru i równo rozłożonych. Wewnętrzne ciśnienie powietrza zmienia wieloboczny kształt w coś bardziej sferycznego. Piłka szybka, lekka, stabilna i przewidywalna. Nic dziwnego, że większość prób zmiany projektu zostało odrzuconych.
Najlepszym sposobem na wkroczenie do akcji jest kilka godnych uwagi przykładów.
Zakręć jak Beckham
Cóż, no tak, oczywiście od tego zaczniemy. Beckhama uznaje się za jednego z najlepszych w historii w sztuce rzutów wolnych. Jego styl był najczystszy w odniesieniu do tego, co wyjaśniliśmy. Żadnych efektów drżenia, pożądanych bądź nie, tylko siła Magnusa o znacznej wielkości, osiągnięta jedynie dzięki jego wyjątkowej umiejętności dodawania wysokiego podkręcenia piłce. W hołdzie, kompilacja kilku goli.
Olimpijski gol
Kolejny klasyczny, lecz bardzo rzadki przykład gola z efektem Magnusa to gol olimpijski. Został tak nazwany po pierwszym golu tego rodzaju strzelonym przez Onzari przeciwko mistrzowi olimpijskiemu, Urugwajowi, w 1924 roku. Został strzelony bezpośrednio z rzutu rożnego. Ponieważ rzut rożny i bramka są w linii prostej strzał nie może zostać oddany prostym kopnięciem. Niektóre z goli zdobywane są dzięki wiatrowi, który pomaga piłce skręcić. Jednak intencją jest zdobywanie bramek tylko z wykorzystaniem efektu Magnusa, przy spokojnym wietrze, istnieje na to tylko jeden sposób:
Piłkarz może posłużyć się dodatkowym efektem psychologicznym przy oddaniu strzału. Wykorzystanie wewnętrznej strony buta jest najprostszym sposobem, aby podkręcić piłkę. Jednak piłkarze mogą strzelać także zewnętrzną stroną, podkręcając piłkę z drugiej strony, więc drużyna przeciwna założy, że piłka skręci w jednym kierunku, lecz ta zrobi to w kierunku przeciwnym. Można to zobaczyć w kilku golach olimpijskich w poprzednim video. Obrońcy zakładają, że piłka zakręci w kierunku od bramki, jednak piłkarz wykorzystuje zewnętrzna stronę buta, aby ją zakręcić w kierunku bramki.
Roberto Carlos, 1997
Lato 1997 roku, Le Tournoi de France był towarzyską rozgrzewką przed Mistrzostwami Świata we Francji w 1998 roku. W meczu otwierającym mistrzostwa, Francja przeciwko Brazylii, Roberto Carlos wykorzystał taktykę opisaną powyżej, podkręcając piłkę w kierunku przeciwnym do oczekiwanego, zakręcając ją wokół muru tak, by strzelić bramkę na miarę arcydzieła:
Jeżeli nie widzicie podkręconej piłki w poprzednim video, zobaczcie gola zdobytego przez Andersona Pico:
Backspin (rotacja wsteczna)
Rotacja wsteczna występuje kiedy piłka obraca się, nie w osi pionowej jak w poprzednim przykładzie, ale w osi poziomej. Siła Magnusa działa wówczas w płaszczyźnie pionowej (tak jak opór i grawitacja). Początkowo pociągnie ona piłkę do tyłu podczas unoszenia, a następnie zadziała odwrotnie kiedy będzie opadać. Prędkość podczas spadania jest niższa, zatem efekt jest mniejszy.
Folha Seca
Drugą stroną monety (rotacji wstecznej) jest Folha Seca (po portugalsku suchy liść). Podkręcenie piłki dodaje siłę Magnusa, w dół. Cristiano Ronaldo jest uznanym mistrzem w tej dziedzinie:
Knuckleball
Czyli piłka rzucona wolno i niepodkręcona: podczas gdy efekt Magnusa jest siłą przewidywalną i zależy od stosunku podkręcenia (ilość podkręcenia względem prędkości piłki), siły drgań wspomniane wcześniej są znacznie bardziej nieprzewidywalne. Jak zostało wyjaśnione, dwa czynniki są odpowiedzialne za ich występowanie. Brak nierówności na powierzchni oraz brak podkręcenia. Obydwa czynniki stabilizują oderwanie warstwy przyściennej sprawiając, że piłka staje się przewidywalna. Kiedy jeden lub obydwa są nieobecne, wówczas występuje nierówne oderwanie, tworząc przypadkowe siły boczne, które sprawiają, że trajektoria jest nieprzewidywalna. Zjawisko to znane jest jako „knuckleball”:
Proszę zauważyć, w drugim linku piłka ledwie się obraca nadając zerową moc sile Magnusa oraz jej oporowi i drżeniu z powodu nierównego oderwania.
Niektórzy mogą pomyśleć, że jako czynnik przypadkowości, knuckleball jest czystym szczęściem. Cóż, wciąż potrzeba sporo umiejętności by zapewnić, po pierwsze, że będzie to knuckleball, po drugie, że jej trajektoria zakończy się zdobytą bramką.
Jest jeden znaczący przykład knuckleball. Na Mistrzostwa Świata w Afryce Południowej, piłka Jabulani została zaprojektowana tak, by była szybsza i bardziej okrągła. Dlatego też została zrobiona z mniejszej ilości, lecz większych i okrąglejszych części, redukując liczbę szwów. To właśnie zły rozkład kilku szwów zmniejszył opór, nadając piłce prędkość, jednak zwiększył drganie, ponieważ oderwanie warstwy przyściennej było mniej stabilne i częstsze. Proszę spojrzeć na bramkę strzeloną Ghanie przez Diego Forlana. Piłka zmienia kierunek na boki około 5 razy, zanim trafi do bramki:
Turbulencja oznacza opór i piłka jest wolniejsza. Turbulencja oznacza również stabilność, zatem istnieje potrzeba odnalezienia dobrego balansu. Mniejsza liczba szwów nie jest odpowiedzią, lecz zmniejsza i zaburza turbulencje. Najnowsze projekty piłek mają mniejszą liczbę szwów, aby stworzyć bardziej okrągły kształt i zwiększyć trwałość piłki. Zamiast standardowego dwudziestościanu ściętego (łaty penta-hexa), najnowsze piłki są dwunastościanami (tylko 12 penta łat), z rowkami imitującymi szwy penta-hexa dwudziestościanu ściętego.
Czy trajektoria jest parabolą?
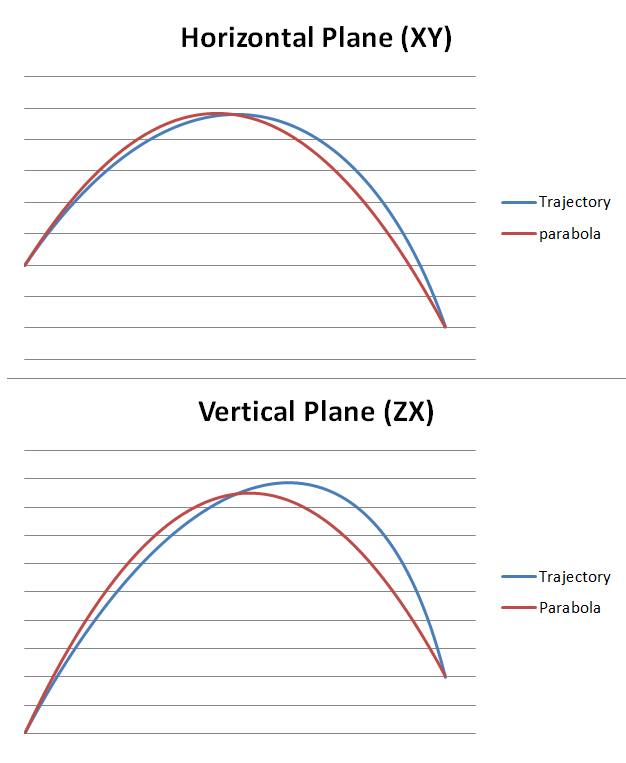
Pozostaje nam zatem ostanie pytanie. Czy słusznym jest nazywanie trajektorii parabolą?
Parabola jest płaską krzywą drugiego stopnia. Podczas integrowania trajektorii przedmiotu podlegającemu tylko stałej sile (na przykład grawitacji), powstaje parabola. Jednakże, jak widać w artykule, nawet w najprostszych przypadkach (brak drgań itp.), na piłkę działają dodatkowe siły, które zależą od prędkości (Magnus i opór). Zintegrowanie trajektorii nie jest łatwym zadaniem i może zostać wykonane jedynie numerycznie. Poniższy rysunek ukazuje trajektorię piłki kopniętej pod kątem przez leworęcznego zawodnika oraz z podkręceniem (niebieski) i jest porównana do paraboli (czerwony). Obydwa wykresy pokazują pionowy i poziomy rzut dwóch krzywych dla lepszego odniesienia.
Trajektoria nie jest parabolą, lecz obie krzywe są relatywnie podobne. Dlatego też, nawet jeśli nie jest poprawnym nazwanie jej parabolą, nadal jest to dość akuratne określenie.
Życzymy wszystkim piłkarzom powodzenia, w obu konkurencjach, żebyśmy mogli cieszyć się dużą liczbą różnego rodzaju goli.
Niech wygrają najlepsi, niech wygrają nasi! Tak, wiemy… Ale nadzieja umiera ostatnia… 😉
A jeżeli zainteresował Cię temat FloEFD lub jakiegokolwiek innego oprogramowania lub szkolenia z naszej oferty, to zapraszamy do kontaktu z nami, chętnie odpowiemy na wszelkie pytania 🙂 Wystarczy kliknąć tutaj i wypełnić formularz kontaktowy.
Opracowanie: Mentor Graphics (Sergio Antioquia) i GM System.