Jak przyspieszyć obliczenia w Femap poprzez zastosowanie elementów RBE2 i GAP w połączeniach sworzniowych?
Jak przyśpieszyć obliczenia w Femap poprzez zastosowanie elementów RBE2 i GAP w połączeniach sworzniowych? Na to pytanie odpowiada poniższy artykuł.
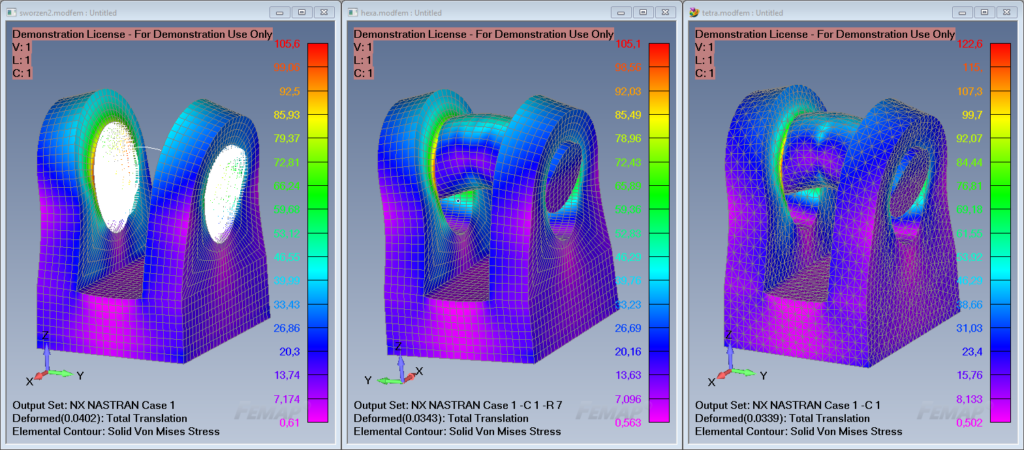
Rys. 1: Porównanie wyników przy zastosowaniu różnych siatek
Przygotowując konstrukcje do obliczeń często spotykamy się z połączeniami sworzniowymi. Możemy sobie z nimi w prosty i szybki sposób poradzić modelując model bryłowo. Wprowadza to jednak zwiększoną liczbę elementów skończonych oraz wymusza stosowanie kontaktów, co przekłada się na czas obliczeń. W Femap możemy zastąpić elementy bryłowe wraz z kontaktami, zastępując sworzeń elementami 1D i stosując elementy GAP jako połączenie sworznia 1D z geometrią otworu.
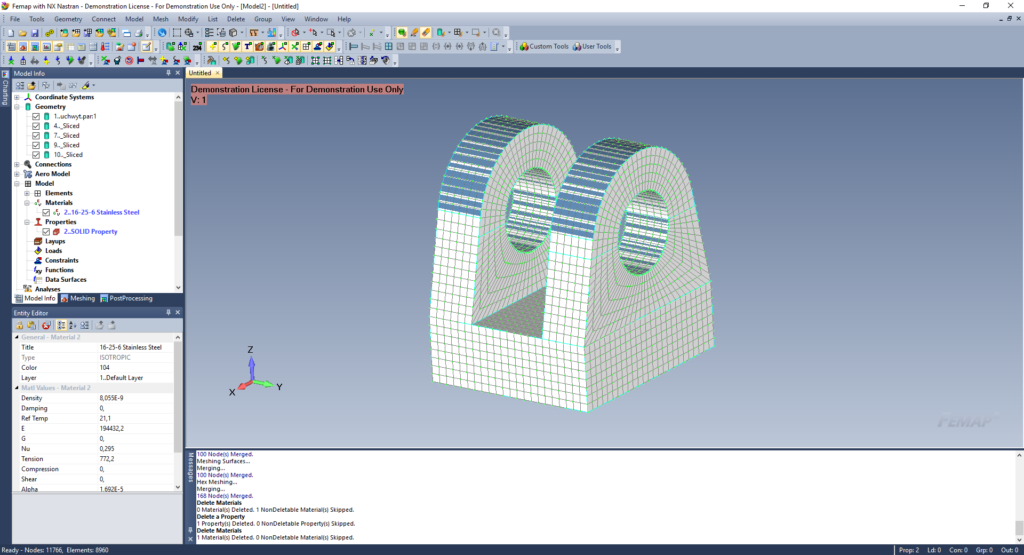
Rys. 2: geometria modelu ze sworzniem
Stworzenie modelu dyskretnego
W przedstawionym modelu stworzono siatkę elementów skończonych dla bryły stosując siatkę typu heksa. Do utworzenia siatki heksahedralnej podzielono wcześniej model na mniejsze obiekty łatwe do zmeszowania.
Rys. 3: podział modelu na mniejsze obiekty
Tak przygotowana geometria jest gotowa do stworzenia siatki. Nadano rozmiar i nałożono siatkę heksa. Do tego celu zastosowano sztuczkę korzystając z narzędzia Meshing Toolbox, dzięki czemu uzyskano ładny rozkład elementów wokół otworów.
Rys. 4: stworzona siatka heksa
W otworach utworzono elementy RBE2, w ten sposób połączyliśmy wszystkie węzły z powierzchni otworu ze środkiem otworu. Elementy RBE2 to elementy sztywne i względnie położenie siatek połączonych przez ten typ elementu nie zmienia się. Usztywniliśmy w ten sposób całą powierzchnię otworu.
Rys. 5: stworzenie elementów sztywnych RBE2
Wstawianie elementów GAP
Taka konstrukcja nie pokaże nam prawidłowego oddziaływania sworznia w otworze. Dlatego pomiędzy końce elementów RBE2 a węzły na powierzchni otworu zostaną wstawione elementy GAP. Są to nieliniowe elementy dwuwęzłowe w przestrzeni trójwymiarowej, które mają różne parametry sztywności na ściskanie, rozciąganie oraz ścinanie. W definicji elementu GAP zdefiniowano dużą sztywność na ściskanie i zerową sztywność na rozciąganie i ścinanie. Dzięki takiemu połączeniu uzyskamy efekt oddziaływania sworznia na detal w miejscu styku i brak naprężeń, gdzie sworzeń będzie „odrywany” od powierzchni otworu. Do stworzenia elementów GAP w odpowiednich miejscach skorzystano z „rozszycia siatki”. Powoduje to oddzielenie siatek tak, aby sąsiadujące elementy skończone nie miały wspólnego węzła. Femap w miejsce rozszycia siatki może wstawić elementy pośrednie i w tym przypadku wskazano elementy GAP.
Rys. 6: wstawienie elementów GAP pomiędzy elementy sztywne a węzły w otworze
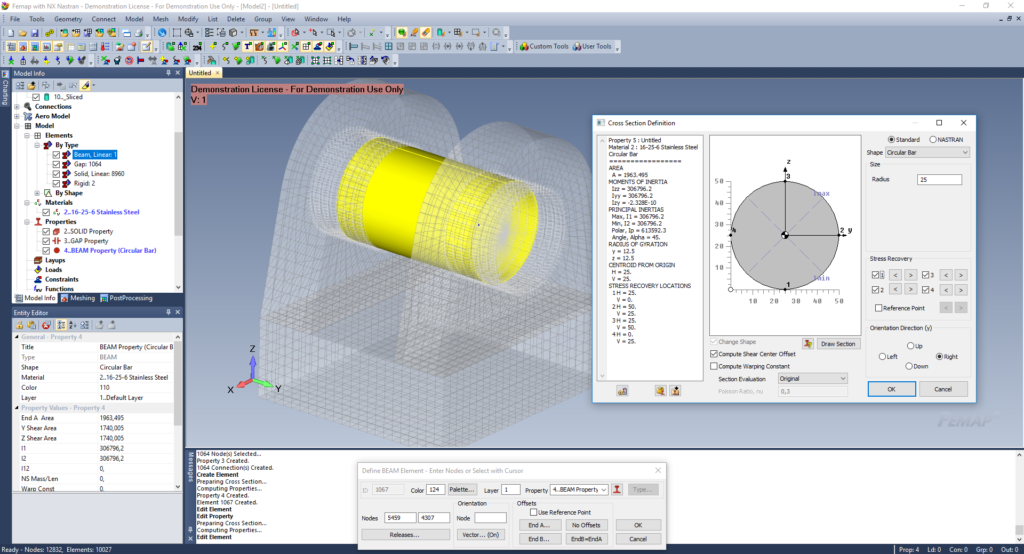
Pomiędzy środkami elementów sztywnych utworzono element belkowy o właściwościach przekroju sworznia.
Rys. 7: wstawienie elementu belkowego
Ponieważ element belkowy został stworzony pomiędzy dwoma węzłami, dodatkowo podzielono długość sworznia na 10 równych odcinków.
Rys. 8: podział elementu belkowego na 10 odcinków
Analiza modelu
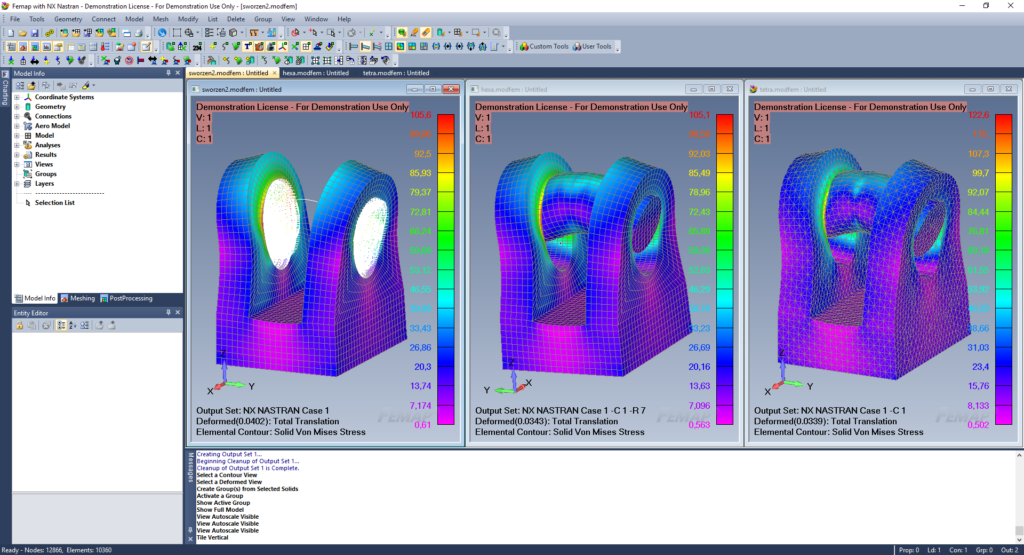
Po nadaniu warunków brzegowych model jest gotowy do obliczeń. W definicji solvera należy zaznaczyć opcję, aby elementy typu GAP były traktowane jako kontakt. To pozwoli na użycie w obliczeniach nieliniowych elementów w analizach liniowych, co jest niewątpliwą zaletą Femap. Wyniki przedstawiono poniżej.
Rys. 9: wyniki analizy sworznia z elementami GAPW
opisany powyżej sposób pokazano jak szybko zamodelować konstrukcję uwzględniając połączenia sworzniowe. Dla porównania dokładności obliczeń przedstawiono wyniki z uwzględnieniem bryłowej reprezentacji sworznia.
Rys. 10: wyniki z uwzględnieniem sworznia jako model 3D
Porównanie wyników i czasów obliczeń
Czas przygotowania i obliczeń ma też niebagatelne znaczenie. Z powodu ograniczenia liczby węzłów oraz zagadnień kontaktowych czas obliczeń został mocno skrócony. Poniżej przedstawiono tabelę z porównaniem wyników dla poszczególnych siatek przy założeniu, że każdy model obliczeniowy zawiera ten sam rozmiar elementu skończonego.
| Model z elementami GAP i BEAM | Model z siatką Hexa | Model z siatką tetra | |
| Liczba węzłów | 12866 | 13909 | 78660 |
| Liczba elementów | 10360 | 10984 | 51689 |
| Maksymalne naprężenia w otworach | 105,6 MPa | 105,1 MPa | 122,6 MPa |
| błąd | 0,5 % | 0 % | 16 % |
| Czas obliczeń | 9.492 seconds | 15.553 seconds | 265.656 seconds |
Rys. 11: porównanie wyników przy zastosowaniu różnych siatek
Opracował: Michał Sroka
Jeśli interesuje Cię program Femap (lub inny program CAE), skontaktuj się z nami.