Wybrane nowości CAD 3D/2D Solid Edge 2022
Cz. 1. Modelowanie powierzchni swobodnych oraz krzywych parametrycznych
Wstęp – co przynosi Solid Edge 2022
Data 6.10.2021. jest szczególnie ważna dla użytkowników popularnego rozwiązania CAD 3D/2D, jakim jest Solid Edge. W tym bowiem dniu swoją światową premierę ma najnowsza generacja tego systemu – Solid Edge 2022.
Według producenta programu – firmy SIEMENS – coroczne premiery jego kolejnych generacji będą od tej chwili miały miejsce właśnie w październiku.
Analizując liczbę i zaawansowanie nowości 3D/2D wprowadzanych do kolejnych wersji tego uznanego rozwiązania CAD – można stwierdzić, że najnowsza generacja Solid Edge 2022 kontynuuje dobry trend, tzn. pakiet przedstawionych tu nowości jest jeszcze bogatszy, niż w wersji poprzedniej. Poza tym, sporo z nich dodano na bezpośrednie życzenie użytkowników.
Publikacja ta (udostępniona dokładnie dzień po światowej premierze systemu) rozpoczyna serię kolejnych artykułów GM SYSTEM, omawiających najciekawsze narzędzia dodane do Solid Edge 2022.
Pierwszy z nich jest poświęcony nowym możliwościom projektowania złożonych kształtów z zastosowaniem powierzchni swobodnych i krzywych parametrycznych.
Modelowanie podziału (ang. subdivision modeling) – nowe sposoby estetycznego łączenia istniejących kształtów
Solid Edge dysponuje od pewnego czasu zestawem potężnych narzędzi do tworzenia i edycji zaawansowanej geometrii powierzchniowo-bryłowej.
Narzędzia te (tworzące pakiet o nazwie „modelowanie podziału”, ang. subdivision modeling) umożliwiają uzyskanie obiektu o pożądanej geometrii (rys. 1b), dzięki łatwej edycji położenia dla płaskich ścianek, liniowych krawędzi oraz węzłów „kratownicy”, w którą można wpisać obiekt w jego bieżącej postaci (rys. 1a).
Najciekawsze nowe funkcjonalności tego pakietu zostaną tu opisane na przykładzie modelowania estetycznej podstawy korpusu dla ekspresu do kawy (rys. 2 – gdzie rejon prowadzonych prac został dodatkowo wyróżniony).
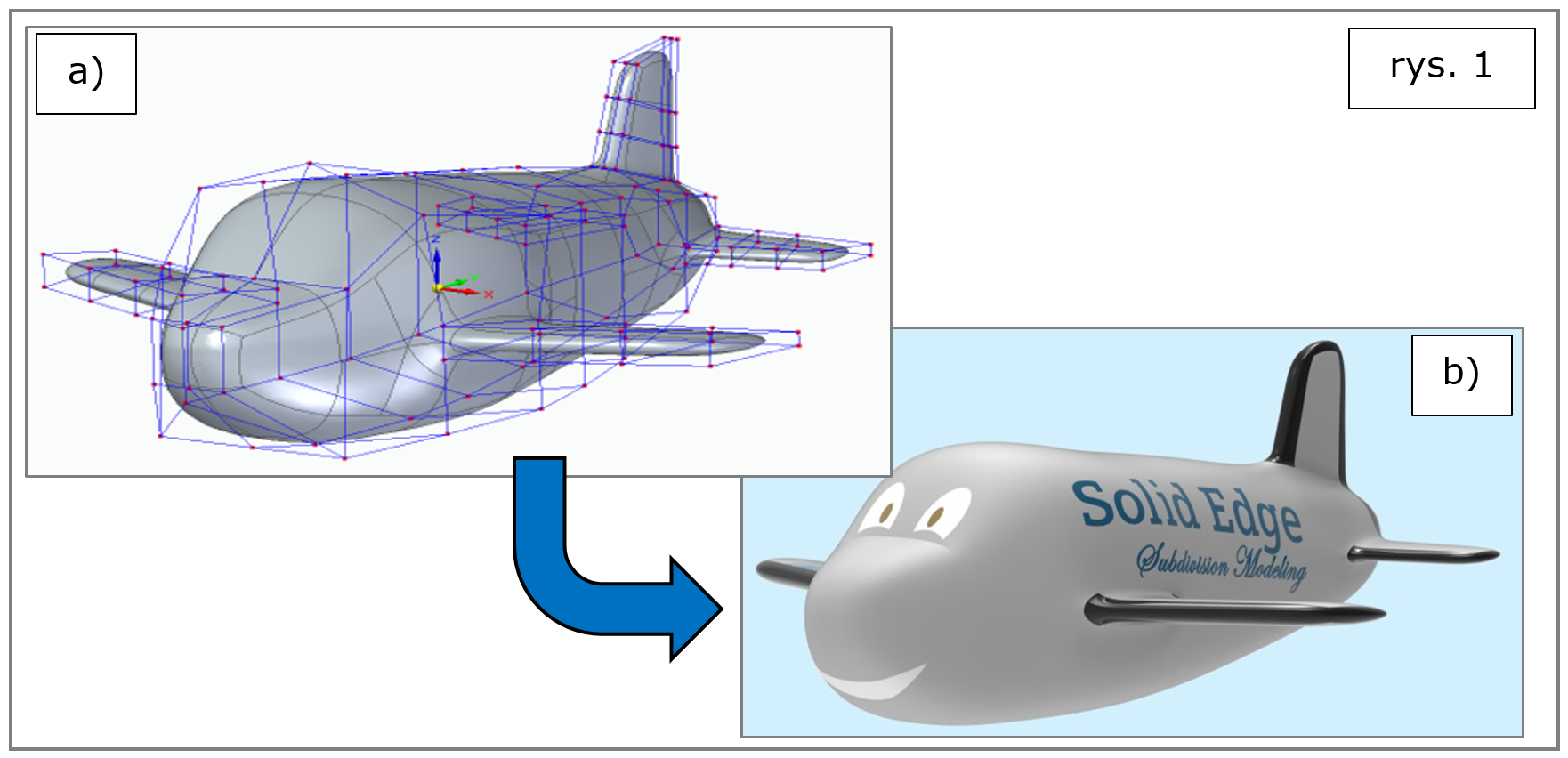
Rys. 1. Modelowanie podziału (subdivision modeling)
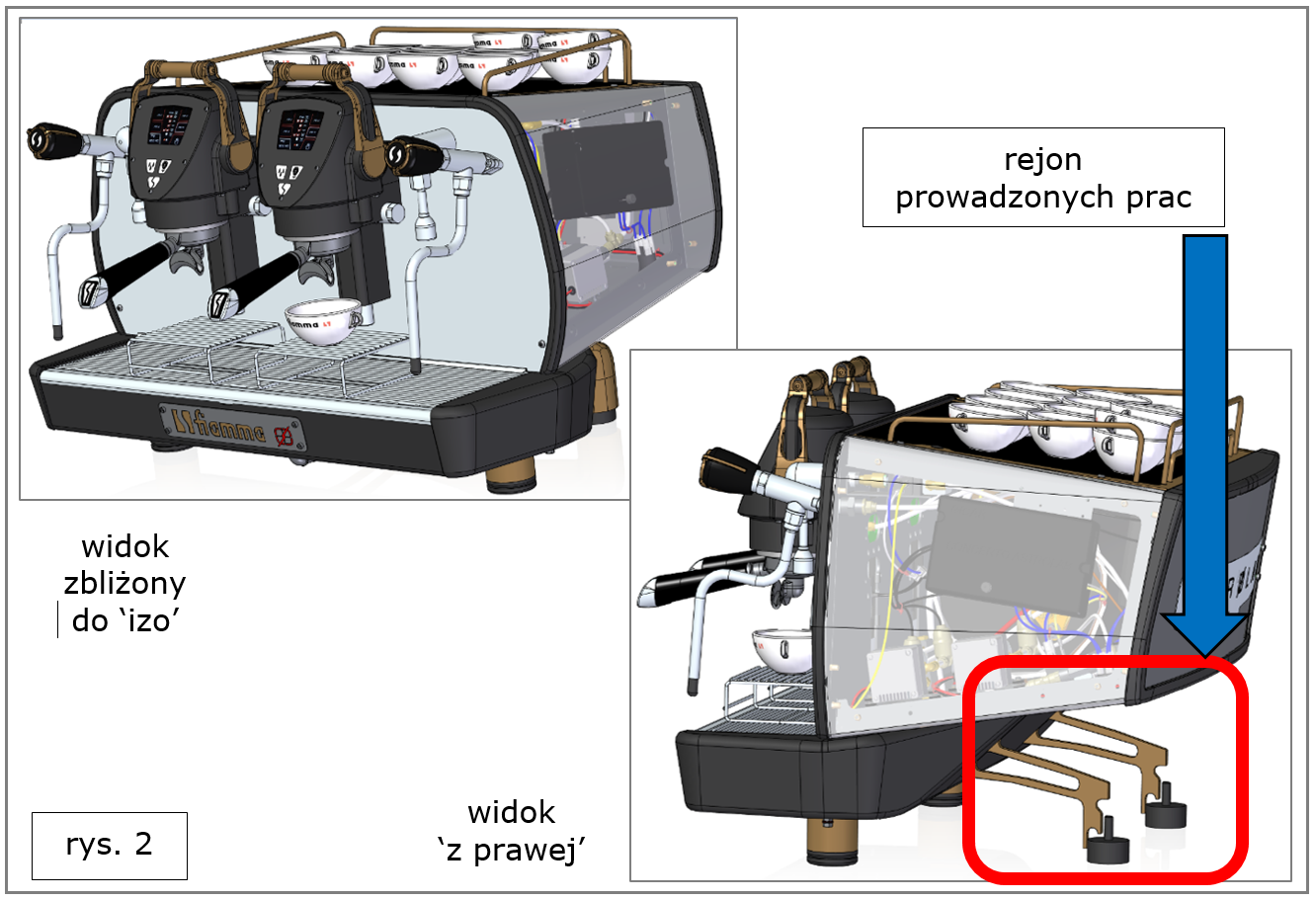
Rys. 2. Solid Edge 2022 – projekt ekspresu do kawy, podstawa korpusu
Działania rozpoczęto od wykonania powierzchniowych filarów tej podstawy o wyjściowym kształcie zbliżonym do dwóch walców (rys. 3a). Filary te wzbogacono o krzywą łączącą wybrane węzły „kratownic” obydwu walców (rys. 3b, gdzie dodatkowo wyróżniono ją żółtą strzałką).
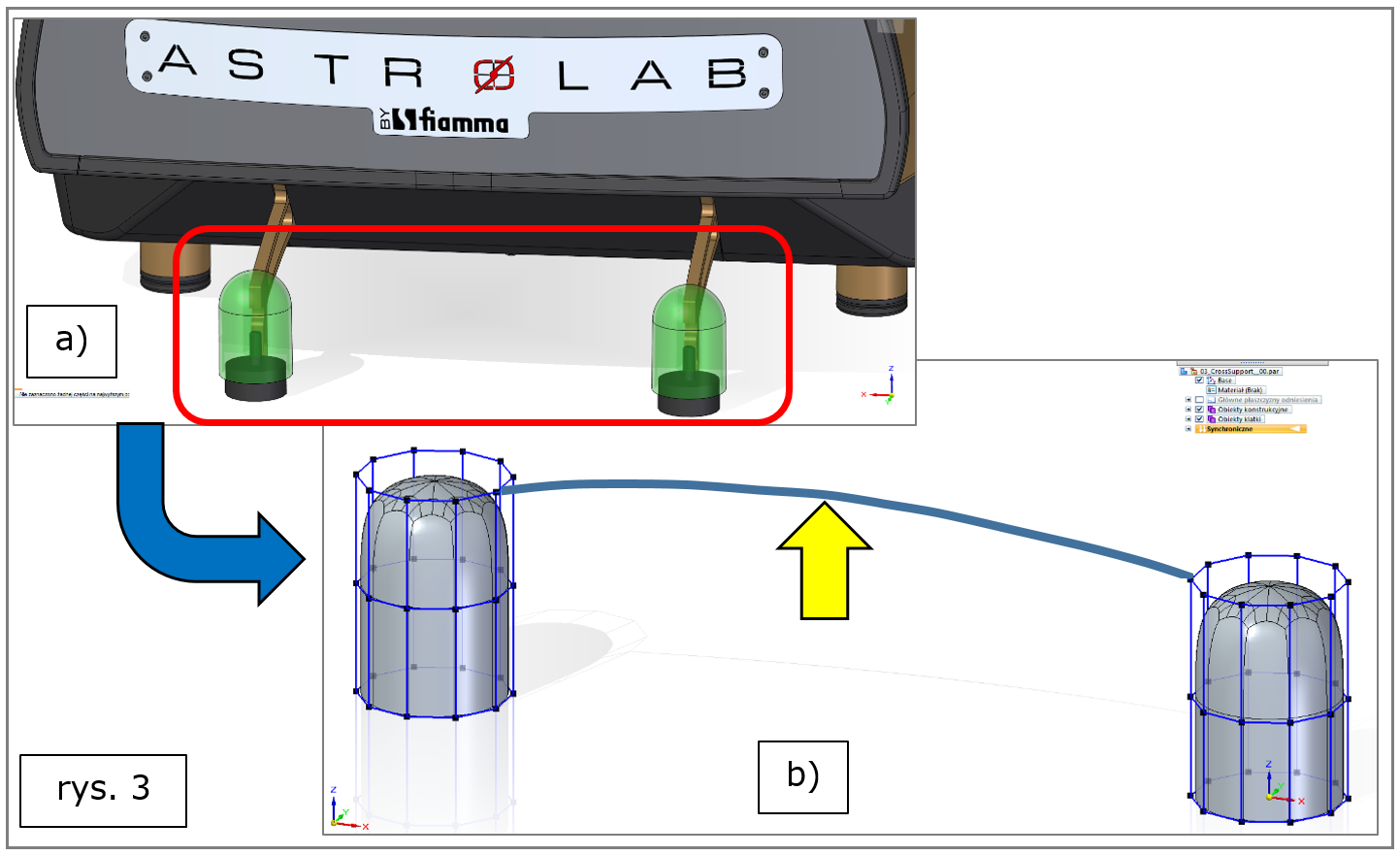
Rys. 3. Solid Edge 2022 – subdivision modeling, rozpoczęcie zadania most wzdłuż krzywej
Solid Edge 2022 umożliwia teraz tworzenie estetycznych „mostów” pomiędzy wybranymi ścianami „kratownic” istniejących już kształtów (rys. 4).
Tutaj jednak oczekuje się jeszcze więcej od geometrii, niż zwykłe połączenie, więc ów powierzchniowy „most” będzie przebiegał wzdłuż zadanej krzywej (rys. 5, który warto porównać z rys. 4).
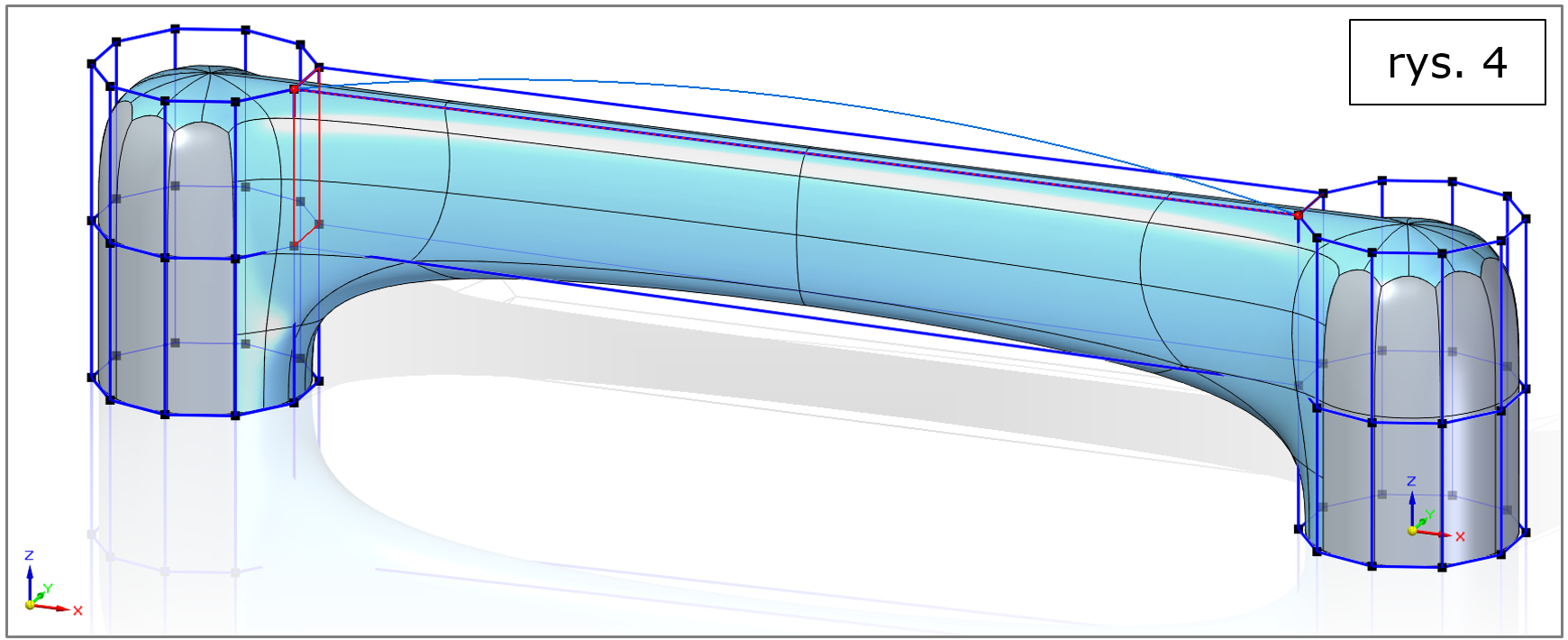
Rys. 4. Solid Edge 2022 – subdivision modeling, most bez krzywej
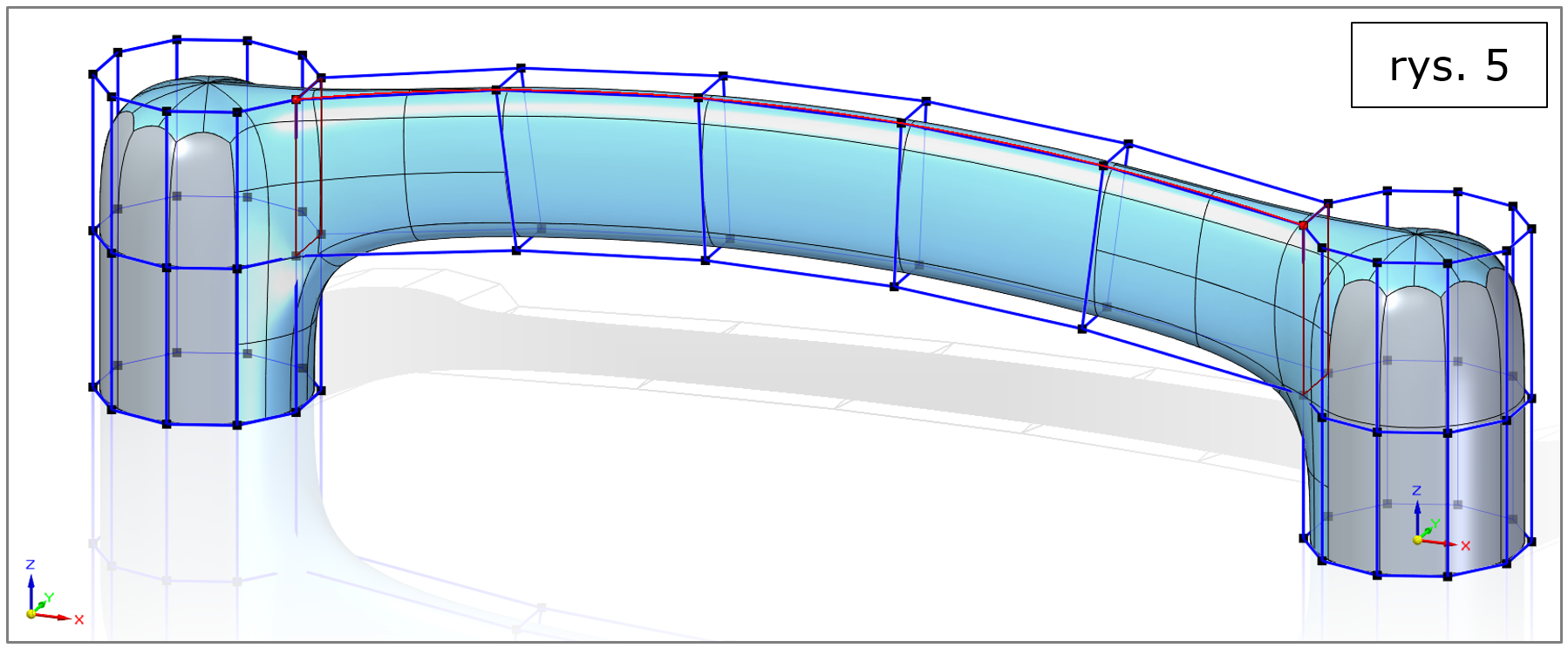
Rys. 5. Solid Edge 2022 – subdivision modeling, most wzdłuż krzywej
Zanim zostaną omówione kolejne prace dotyczące kształtu modelowanej podstawy, warto na chwilę zatrzymać się w tym miejscu i zaprezentować inne przykłady uzyskiwania omawianych „mostów”:
– łącząc wybrane ściany „kratownic” dwóch pierścieni (rys. 6a) można szybko uzyskać wynikową geometrię, jak na rys. 6b (wyrób z branży zabawek),
– w zależności od lokalizacji łączonych ścian i opcjonalnego zastosowania krzywej prowadzącej – edycja może polegać na modyfikacji modelu (rys.7a) przez jego rozbudowę do wewnątrz (rys.7b) lub na zewnątrz (rys.7c); w obu przypadkach uzyskane modele są właściwe dla branży jubilerskiej,
– prowadząc wzdłuż wskazanej krzywej zaledwie jedną ściankę „kratownicy” (tj. definiując ściankę „startową” i rezygnując ze wskazania „końcowej’), czyli wychodząc z modelu jak na rys. 8a można docelowo uzyskać kształt z rys. 8b, właściwy m.in. dla wyrobów typu rękojeść, uchwyt, czy klamka (warto porównać te obrazy z rys. 3b i rys. 4).

Rys. 6. Solid Edge 2022 – subdivision modeling, mosty powierzchniowe, pierścienie
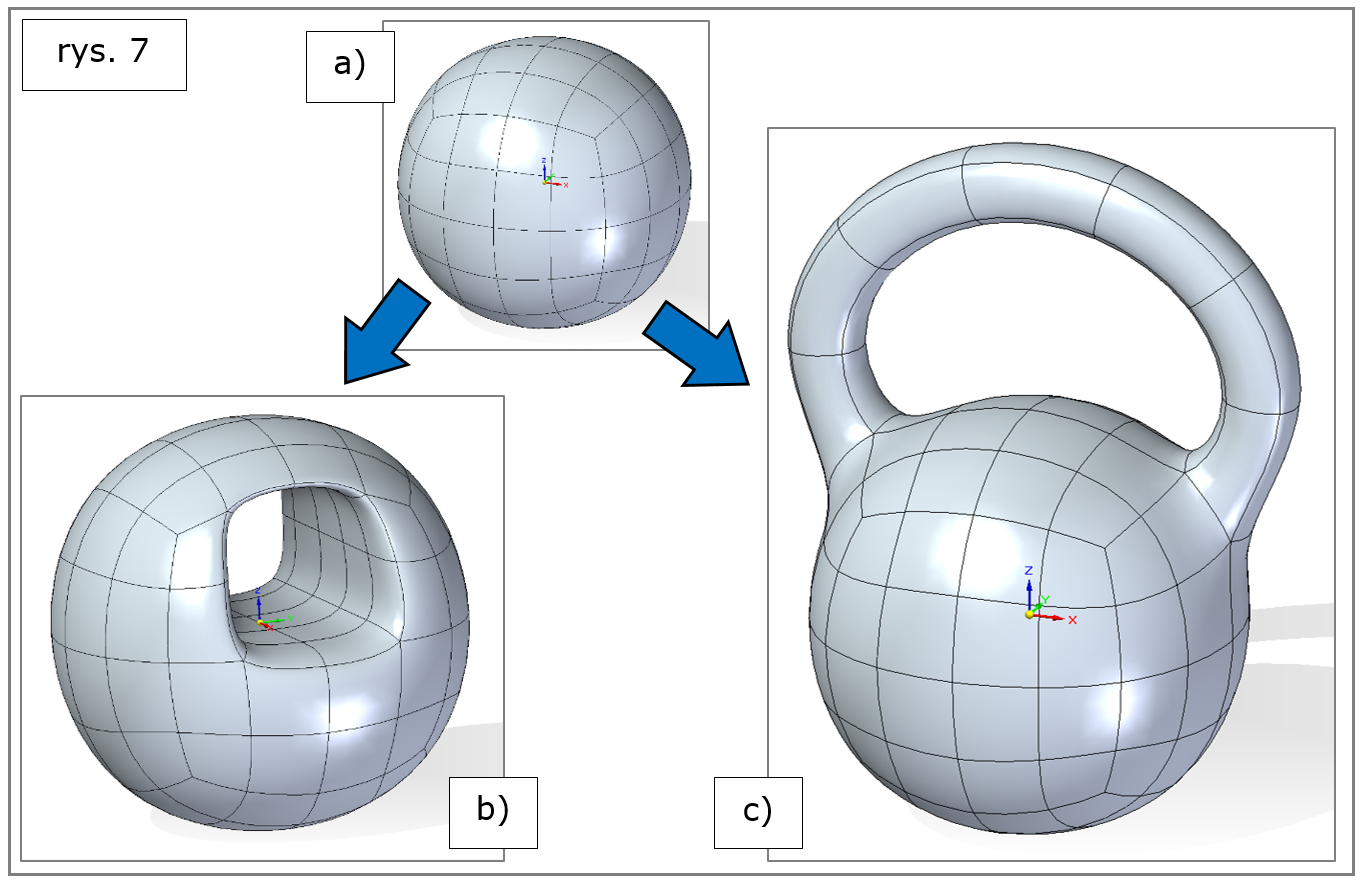
Rys. 7. Solid Edge 2022 – subdivision modeling, mosty powierzchniowe, kula
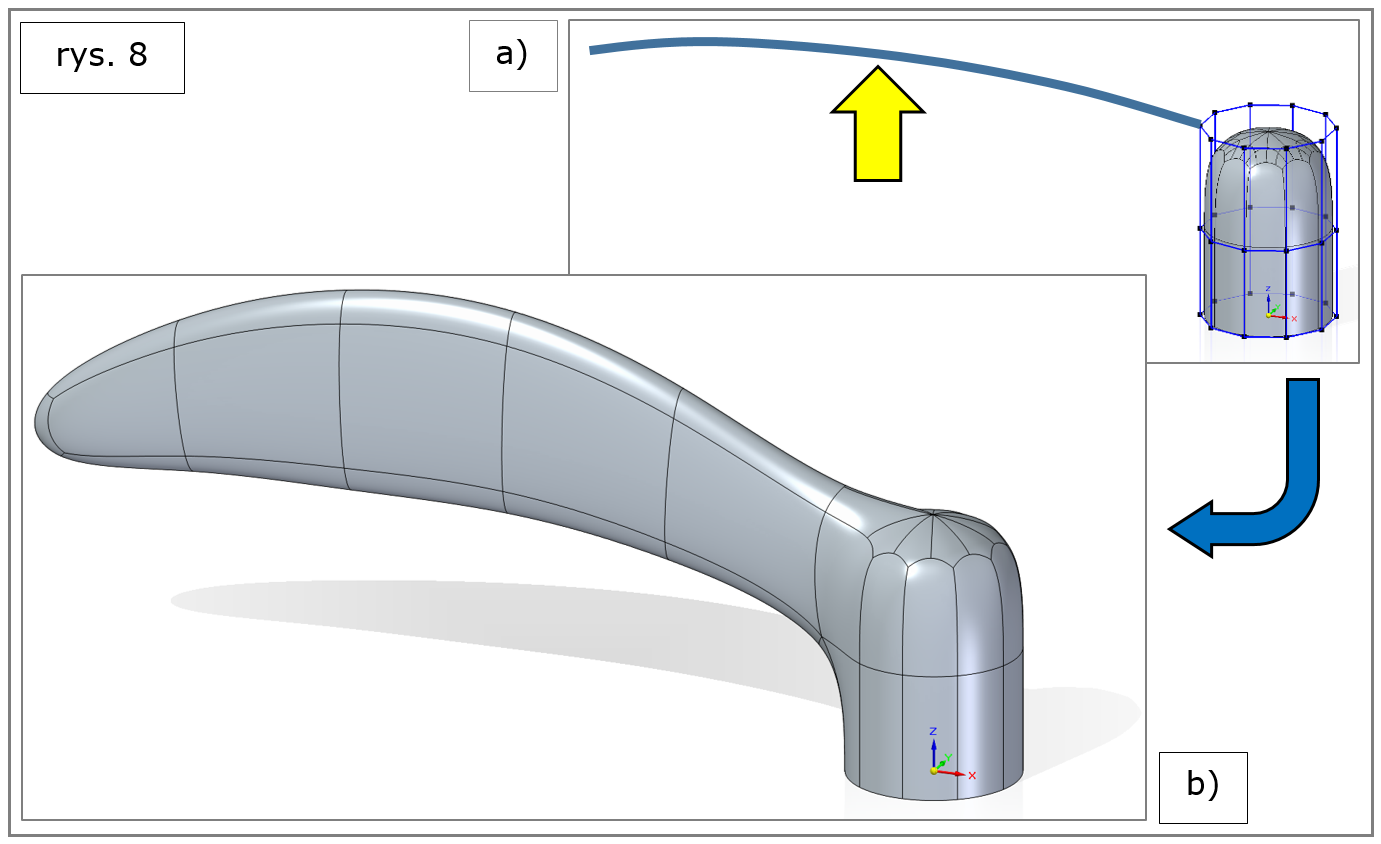
Rys. 8. Solid Edge 2022 – subdivision modeling, most powierzchniowy, uchwyt
Wyrównywanie wskazanych węzłów „kratownicy” do zadanej krzywej
Model projektowanej podstawy ekspresu do kawy zaopatrzono w jeszcze jedną krzywą, leżącą na płaszczyźnie pokrywającej się z podstawami „walców”, jak na rys. 9 (widok zbliżony do izometrycznego) oraz rys. 10a (widok „z góry”).

Rys. 9. Solid Edge 2022 – subdivision modeling, wyrównanie do krzywej, rozpoczęcie, podstawa
Użytkownik Solid Edge 2022 może teraz zażądać, aby wybrane węzły „kratownicy” zostały dosunięte do wskazanej krzywej, z założeniem określonego kierunku tej modyfikacji (jak na rys. 10a, gdzie ów kierunek przedstawiono czerwoną strzałką).
Efekt tych działań zilustrowano na rys. 10b.
Idąc dalej, węzły leżące na „przeciwległej” ścianie uchwytu (względem węzłów wyróżnionych na rys. 10a) można także wyrównać do krzywej (a nawet kilku krzywych) utworzonych doraźnie tu i teraz, wręcz rysowanych na ekranie i to różnymi metodami (rys. 11a).
Oczekiwany skutek powyższego przedstawiono na rys. 11b.
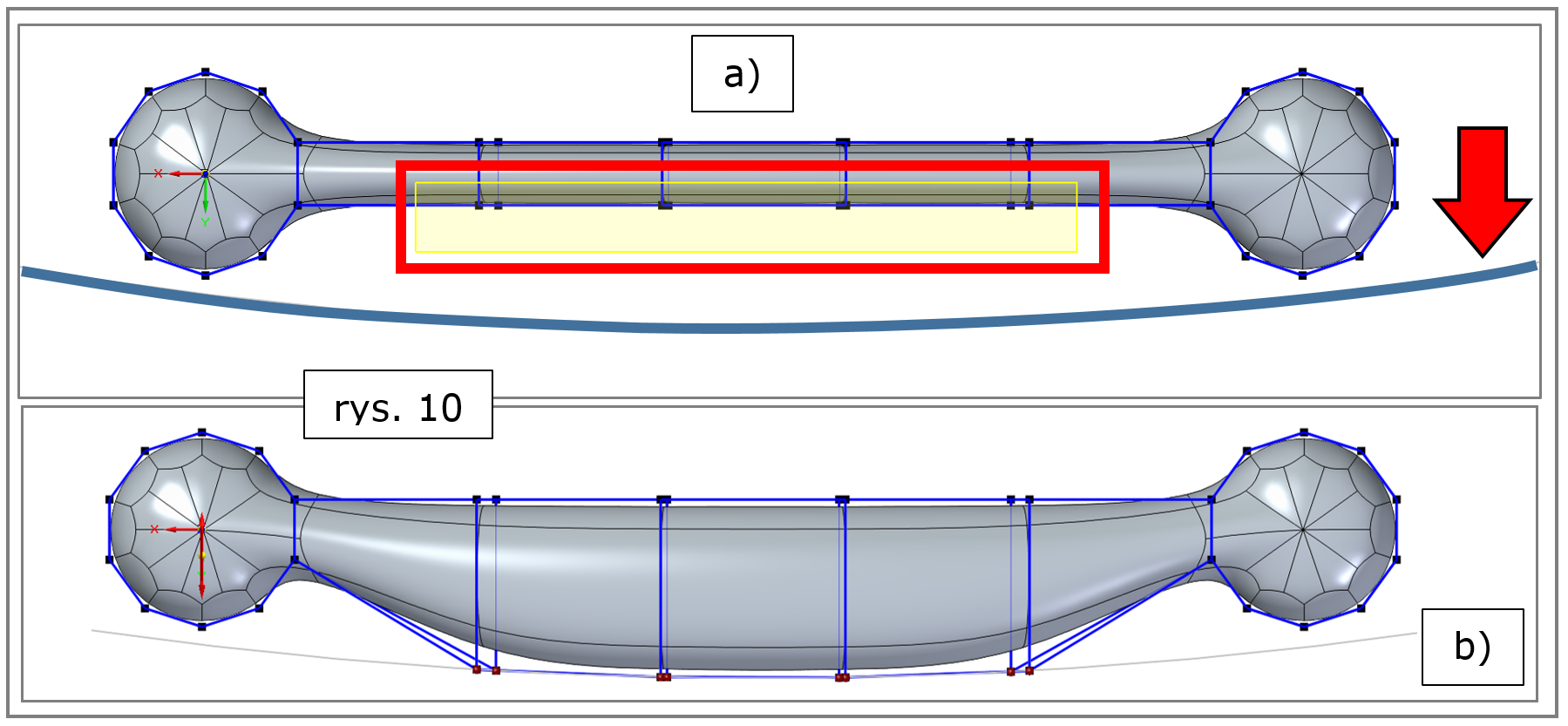
Rys. 10. Solid Edge 2022 – subdivision modeling, wyrównanie do krzywej, wskazanie
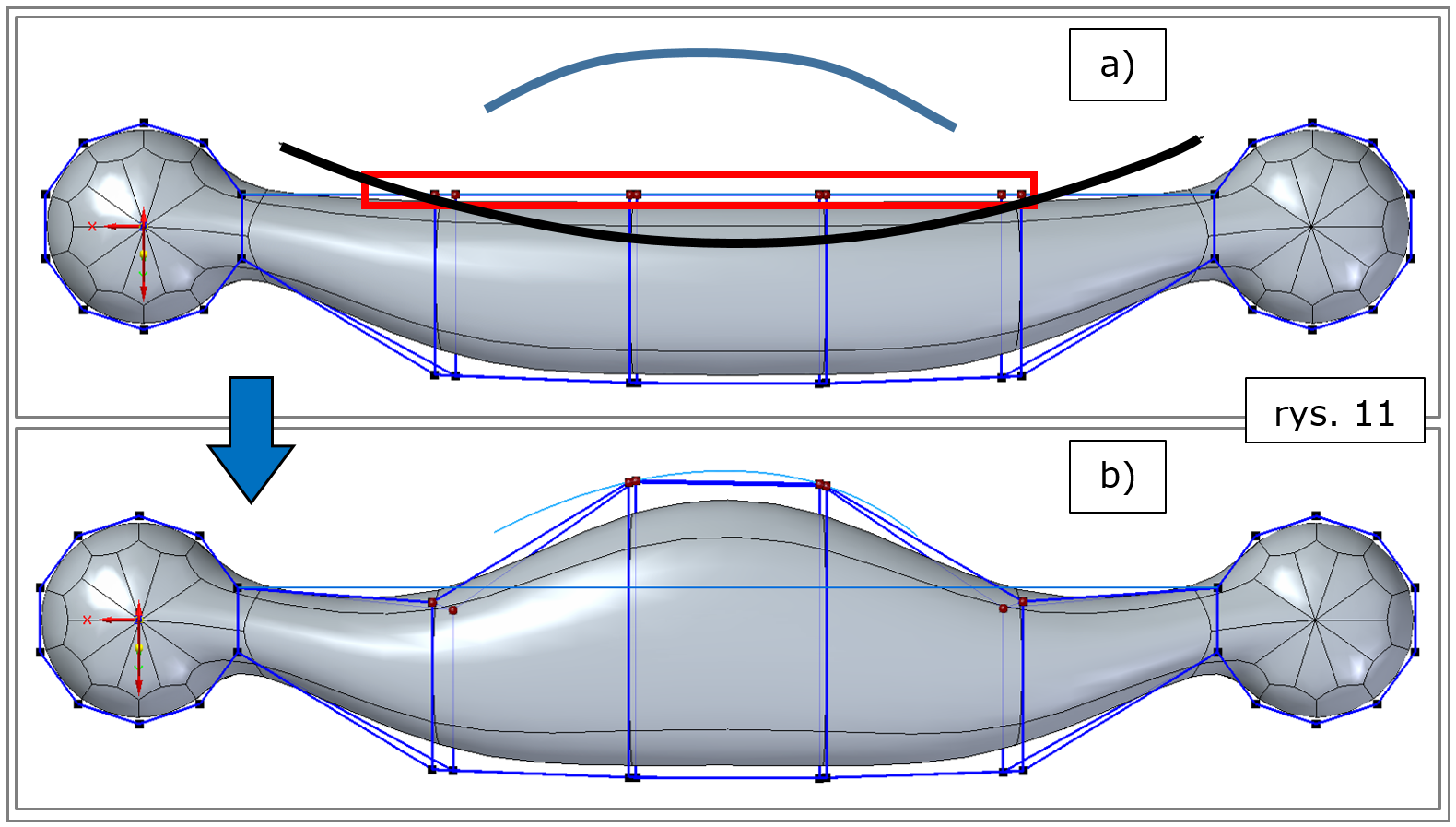
Rys. 11. Solid Edge 2022 – subdivision modeling, wyrównanie do krzywej, narysowanie
Korzystając z przedstawionych tu nowych rozwiązań, łatwo utworzono finalny model eleganckiej podstawy dla korpusu ekspresu do kawy (rys. 12a – widok z góry, rys. 12b – widok zbliżony do izometrycznego).
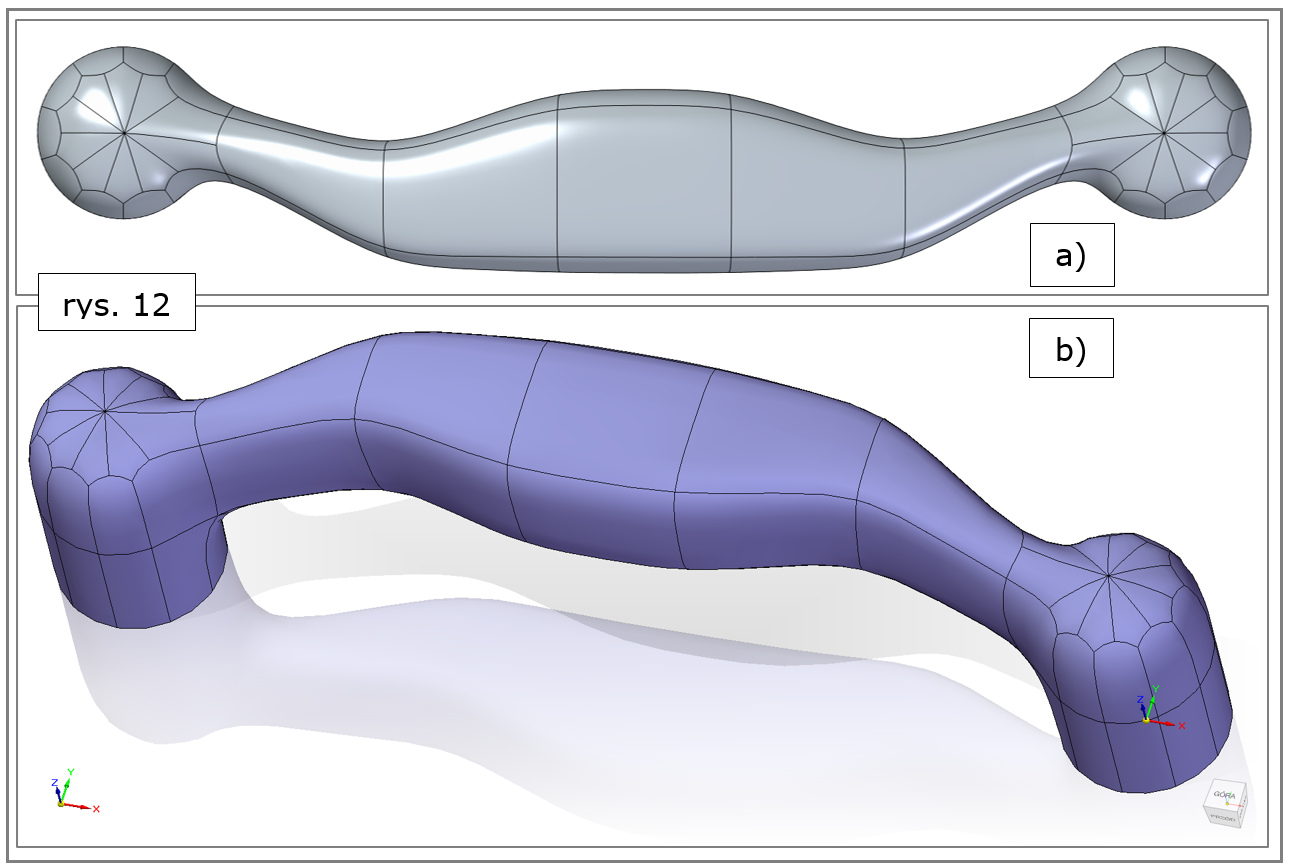
Rys. 12. Solid Edge 2022 – subdivision modeling, efekt finalny, podstawa korpusu
Korzystnie stosując przedstawione narzędzia można szybko przekształcać nieskomplikowaną geometrię początkową (rys. 13) do postaci zaawansowanej (rys. 14).
Na rys. 13 widnieje „walec” o mocno zaokrąglonych krawędziach podstaw, rozbudowany o krzywe reprezentujące jego docelowe zarysy z różnych stron (obiekt przedstawiono w widoku zbliżonym do izometrycznego).
Na rys. 14 zilustrowano natomiast efekt ciekawej modyfikacji tegoż „walca”. Uzyskano tu projekt estetycznego korpusu pilota zdalnego sterowania (przedstawiony z widoku „izo” i obróconym względem niego o 90° wzgl. osi Y).
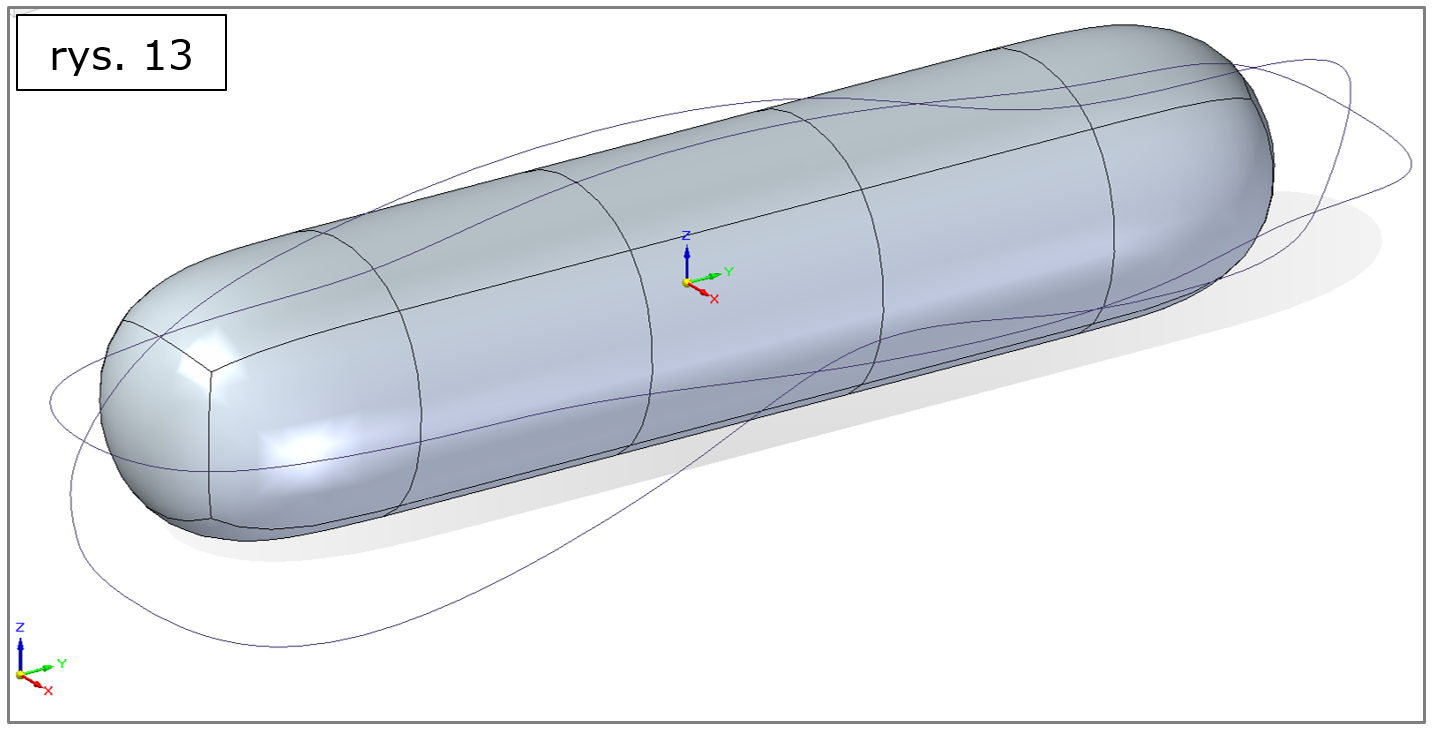
Rys. 13. Solid Edge 2022 – subdivision modeling, wyrównanie do krzywej, rozpoczęcie, pilot
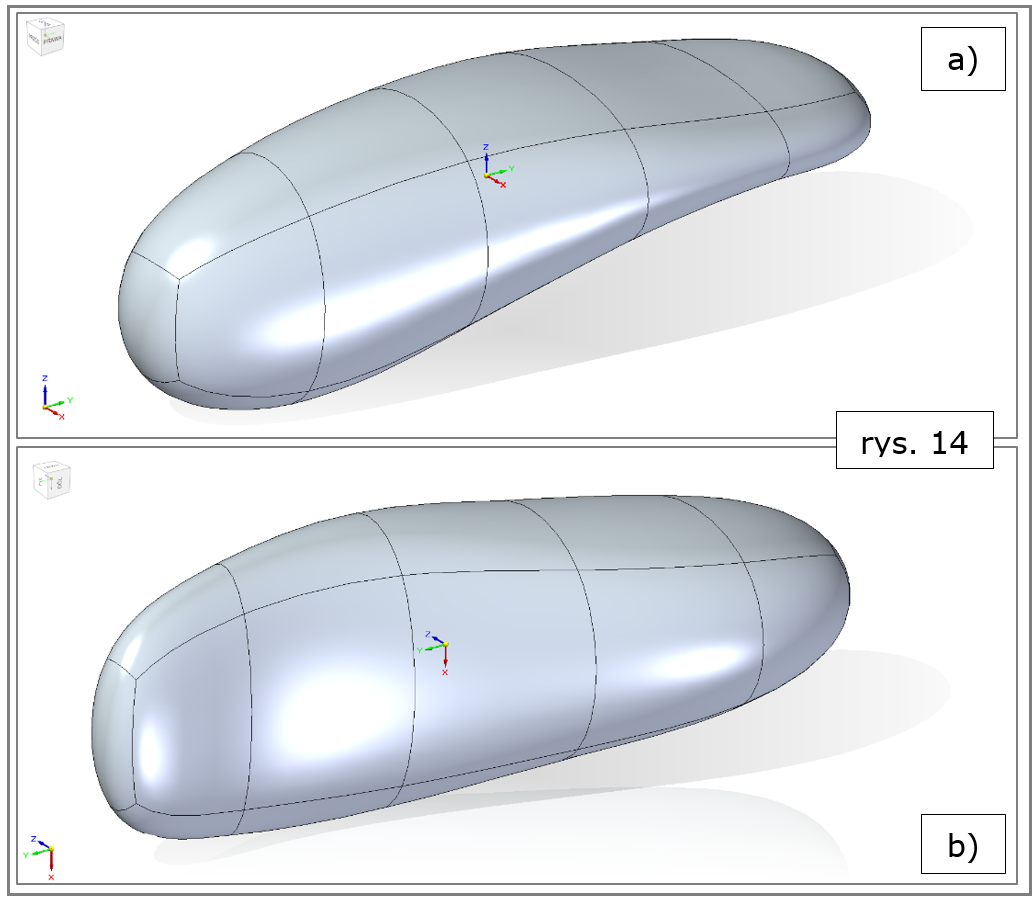
Rys. 14. Solid Edge 2022 – subdivision modeling, wyrównanie do krzywej, efekt finalny, pilot
Odsunięcia ścian „kratownicy”
Solid Edge 2022 pozwala teraz na łatwe i dwustronne odsunięcia ścian „kratownicy” na kierunkach do nich normalnych. Łącząc tę funkcjonalność z różnymi metodami przebudowy obiektu – można uzyskać modyfikację przykładowego modelu z rys. 15a do różnych postaci wynikowych (rys. 15b,c). Na rysunkach tych modyfikowane fragmenty (odsuwane „do wewnątrz” i „na zewnątrz”) wyróżniono kolorystycznie.
Ważne jest również to, że polecenia odsunięcia mogą teraz współdziałać także z poleceniami do postępujących podziałów „kratownicy”, tj. stopniowego jej ‘zagęszczania’, in. zwiększania liczby jej krawędzi dla podniesienia stopnia złożoności projektowanego obiektu.
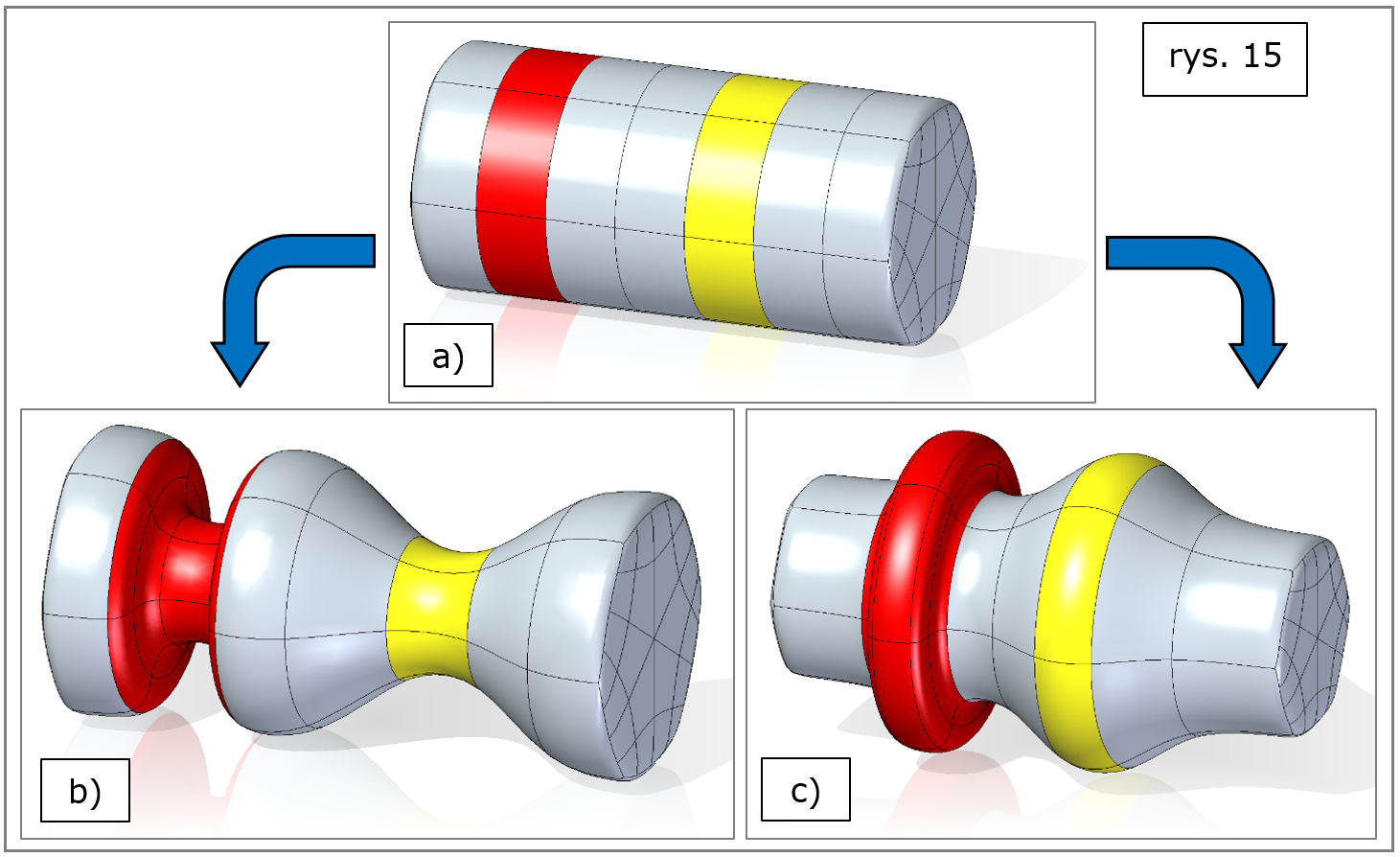
Rys. 15. Solid Edge 2022 – subdivision modeling, odsunięcia
Rozbudowa narzędzi do edycji krawędzi „kratownic otwartych”
W najnowszym Solid Edge 2022 krawędzie „kratownic otwartych” – jak np. krawędzie obiektu powstałego jako część modelu sfery, rys. 16 – mogą zostać poddane edycji w sposób analogiczny jak dla ścian.
Mowa tu o wykorzystaniu funkcjonalności typu Podnieś (główna nowość) oraz Utrzymuj powierzchnię, czego efekty przedstawiono na rys. 17.
Po kilku kolejnych szybkich działaniach omawianego typu otrzymać można model przydatny do modelowania i formowania jednorazowych łyżeczek dla ich produkcji (rys. 18), naturalnie z materiałów ekologicznych.
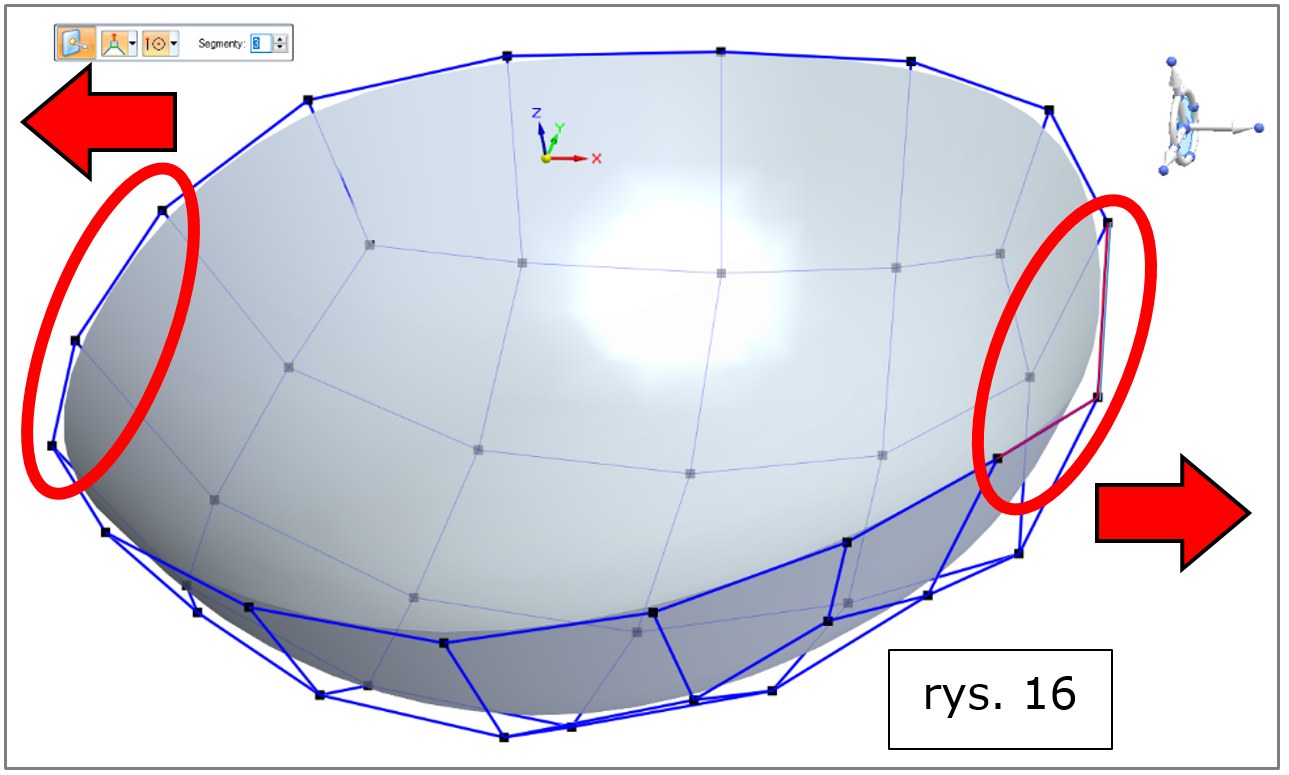
Rys. 16. Solid Edge 2022 – subdivision modeling, krawędzie otwarte
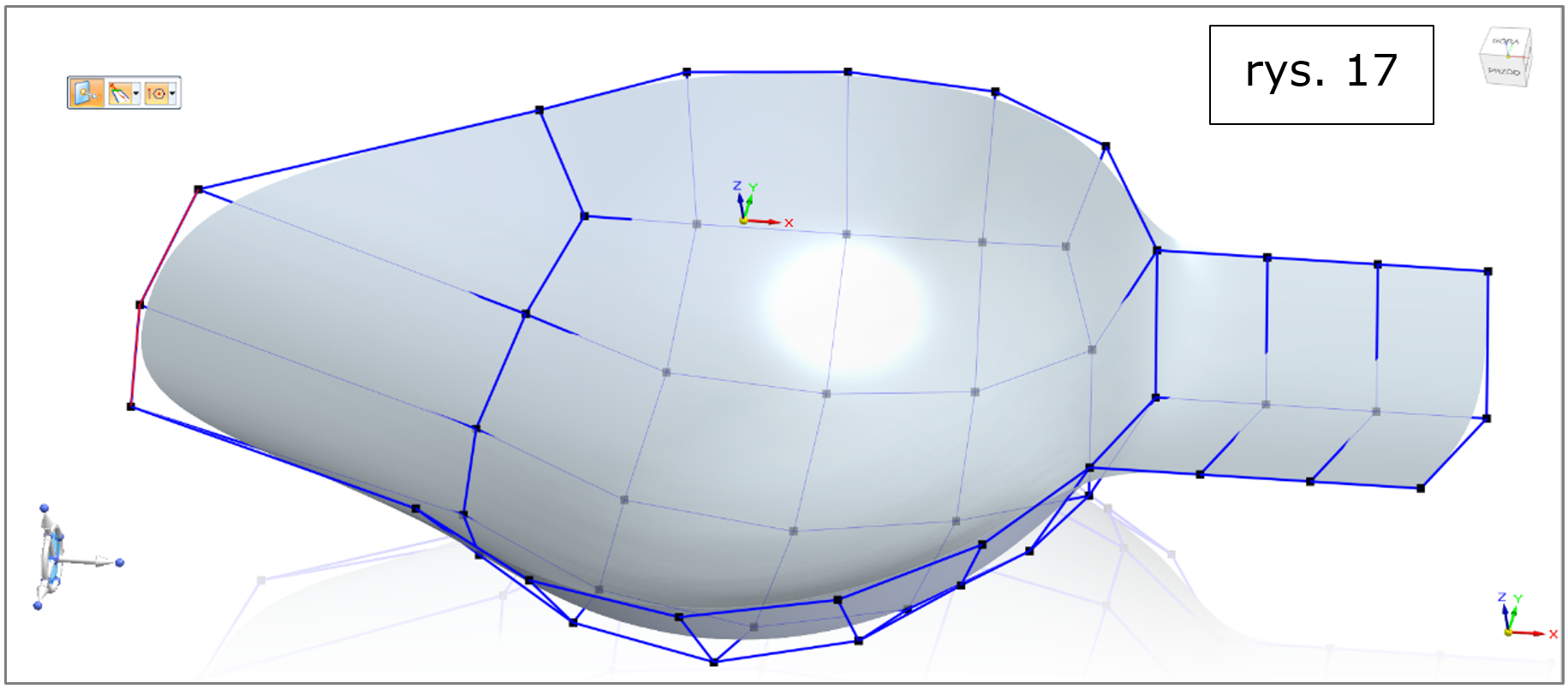
Rys. 17. Solid Edge 2022 – subdivision modeling, krawędzie otwarte, podnieś – utrzymuj

Rys. 18. Solid Edge 2022 – subdivision modeling, krawędzie otwarte, efekt finalny, łyżka
Wykreślanie krzywych parametrycznych dla ich wykorzystania w operacjach powierzchniowo – bryłowych
Solid Edge 2022 oferuje zbiór poleceń oczekiwanych przez wielu projektantów specjalizujących się w modelowaniu z wykorzystaniem tzw. krzywych analitycznych z parametrem, zwanych potocznie „krzywe parametryczne”.
W dużym uproszczeniu – krzywa taka to ciągły zbiór punktów, gdzie wartości współrzędnych X, Y, Z mogą być następującej postaci:
– zmienna, czyli są to wyniki określonych działań matematycznych, realizowanych na podstawie rosnącego parametru t, w jego określonym przedziale, np.:
X = t * cos (t),
Y = t * sin (t),
dla t w przedziale od 0 do 2*PI, co w połączeniu z poniższym Z=0 daje tzw. spiralę Archimedesa, jak na rys. 19
– stała (np. Z = 0 dla wszystkich argumentów funkcji dla uzyskania krzywej płaskiej leżącej na płaszczyźnie XY „Góra”, ew. Z = 5, by leżała ona na płaszczyźnie równoległej do XY, odległej o 5 „na kierunku +Z”
Chcąc krzywą z rys. 19 np. rozciągnąć w osi X / spłaszczyć w Y i obniżyć o 10 w Z powyższe wyrażenia można zmienić, wprowadzając odpowiednie stałe, np.
X = 3 * t * cos (t),
Y = 0,5 * t * sin (t),
Z = -5
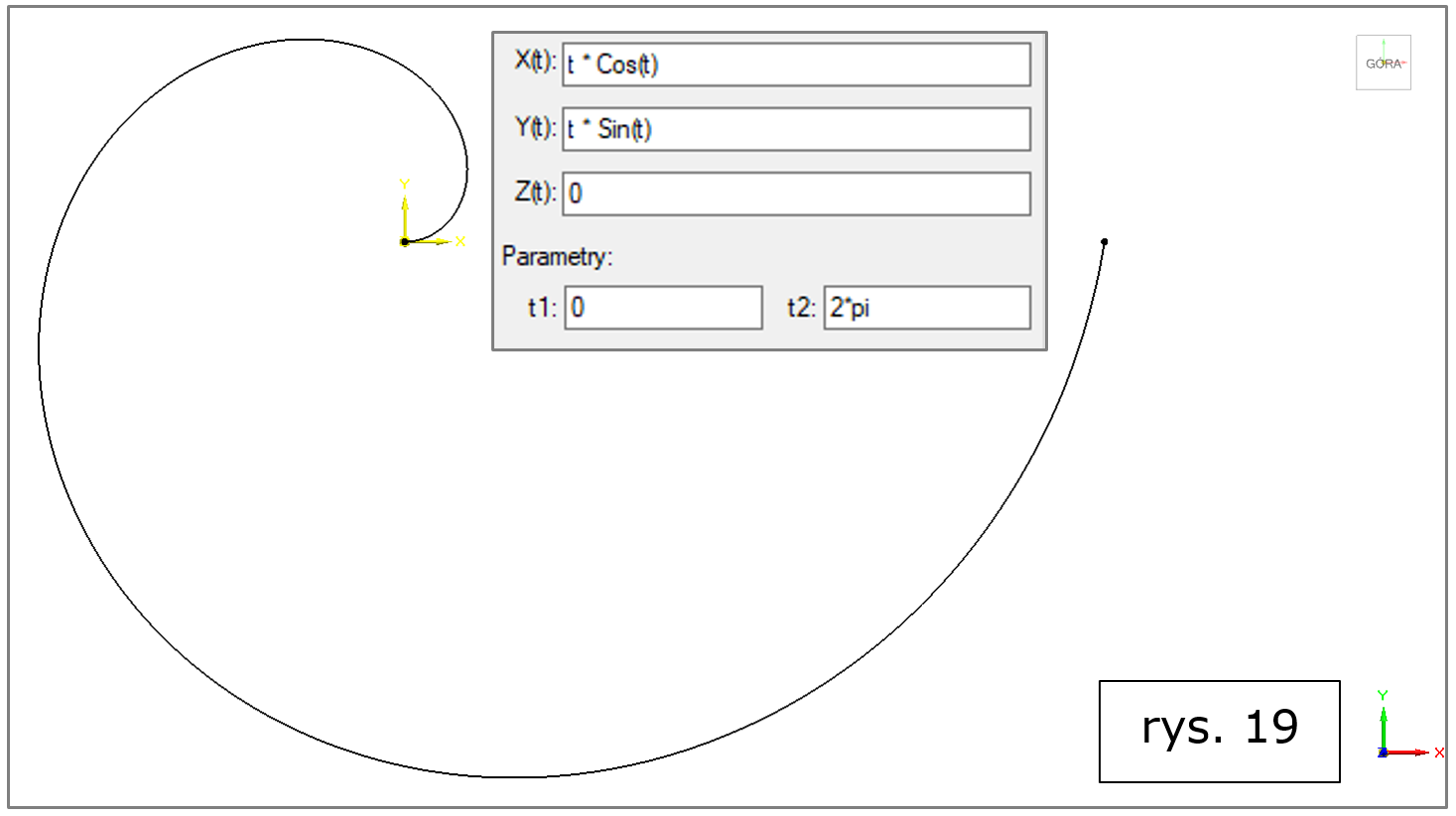
Rys. 19. Solid Edge 2022 – krzywa wynikowa równania, spirala Archimedesa
Pracując z nowymi narzędziami, użytkownik Solid Edge 2022 jest w stanie utworzyć w zasadzie dowolną krzywą, którą można wyrazić w powyższy sposób.
Warto zauważyć, że dana krzywa może zostać zapisana w systemie dla jej łatwiejszego stosowania w przyszłości, a także wprowadzona
na odpowiednio wybranym układzie współrzędnych.
Aby jednakże ułatwić zadania projektowe, w Solid Edge 2022 występuje wiele krzywych uprzednio zdefiniowanych i gotowych do natychmiastowego użycia (pamiętajmy, że mogą one domyślnie zawierać także dodatkowe zmienne / stałe, dla ich przyspieszonej ewentualnej modyfikacji).
Zestawiono je tutaj w porządku alfabetycznym (rosnąco wg umownej nazwy):
a) epicykloida
b) epitrochoida
c) ewolwenta
d) hipocykloida
e) hipotrochoida
f) krzywa Lissajou,
g) krzywa łańcuchowa
h) krzywa o kształcie podkładki sprężystej
i) krzywa Steinmetz’a
j) krzywa Viviani’ego
k) lemniskata Bernoulli’ego
l) linia
m) rozkład normalny
n) spirala Archimedesa
o) spirala logarytmiczna
p) spirala stożkowa
q) spirala walcowa
r) spirala Slinky
s) ślimak Pascala
t) traktrysa
u) trochoida
v) tryg. cosinusoida
w) tryg. sinusoida
Kilka z tych krzywych zostanie tu nieco bliżej przedstawionych, ze względu na niektóre inżynierskie aspekty ich stosowania (warto zwrócić uwagę na stosowane wyrażenia dla wartości X, Y, Z, zarówno jako f(t) oraz jako stałe, co zostało przedstawione w oknach dialogowych na poniższych obrazach):
– kinematyka maszyn i mechanizmów:
ad a) epicykloida (rys. 20, więcej informacji także TUTAJ),
ad p) spirala stożkowa (rys. 21, więc informacji także TUTAJ)
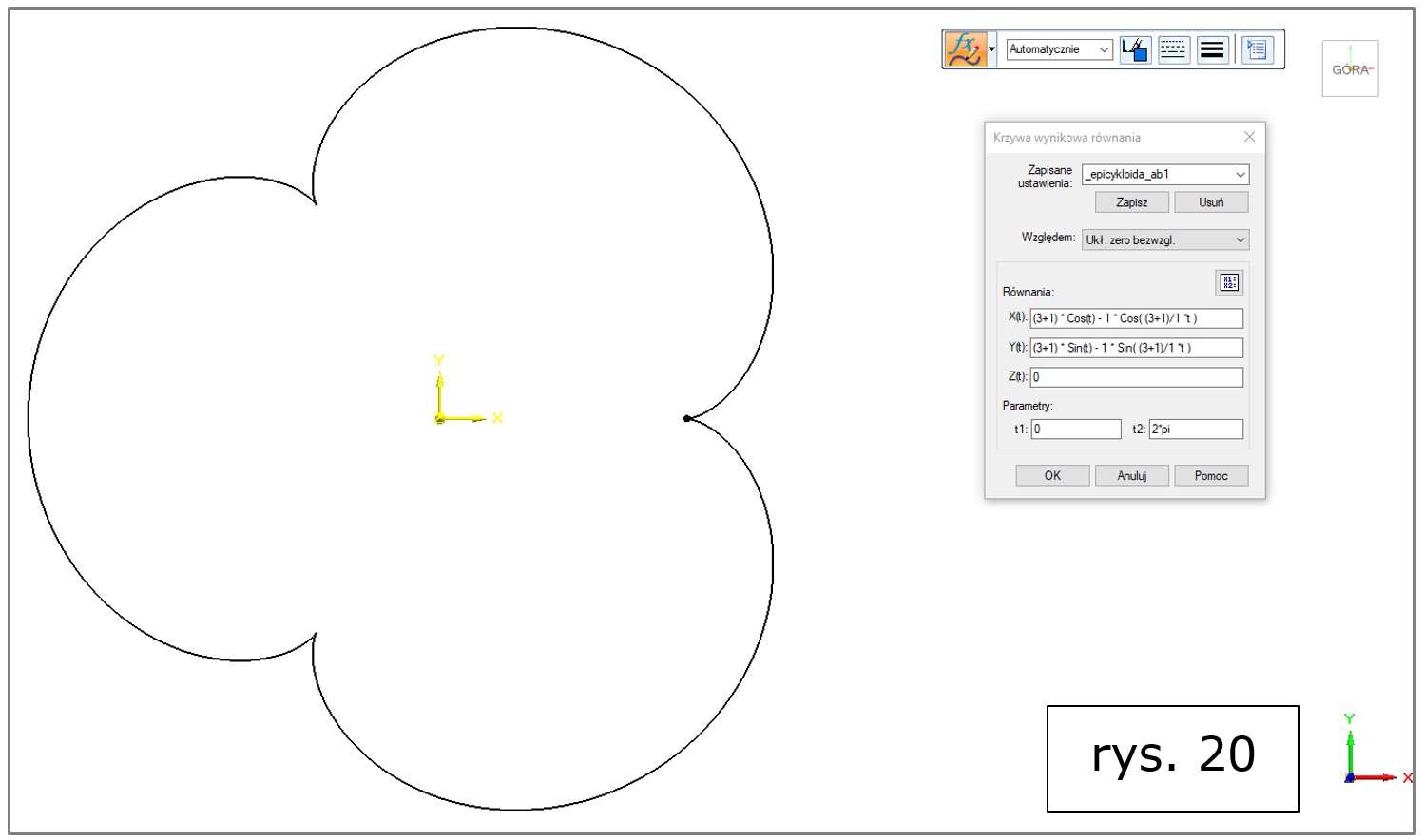
Rys. 20. Solid Edge 2022 – krzywa wynikowa równania, epicykloida
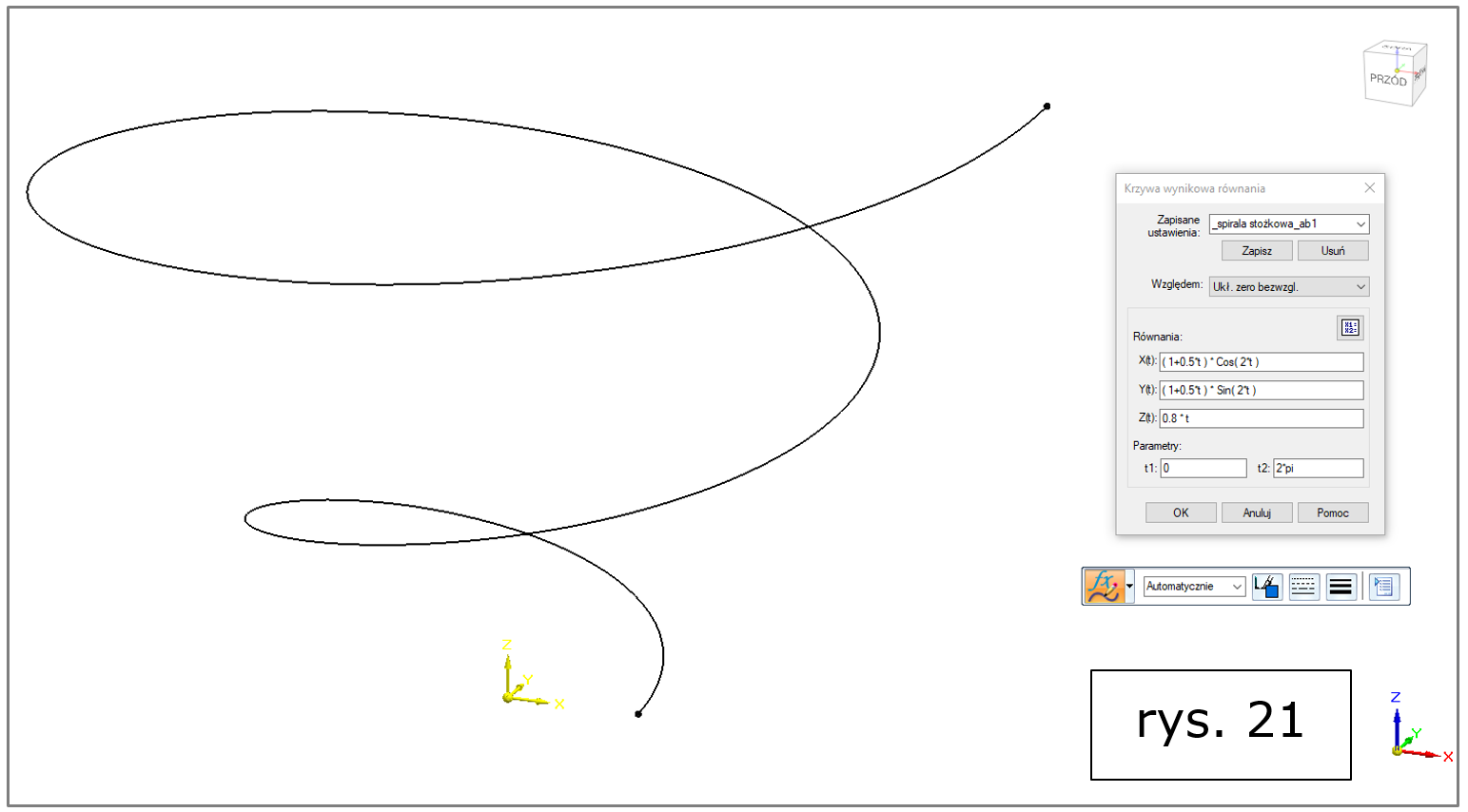
Rys. 21. Solid Edge 2022 – krzywa wynikowa równania, spirala stożkowa
– budowa i technologia maszyn:
ad c) ewolwenta (rys. 22, więcej informacji także TUTAJ),
ad u) trochoida w ujęciu ogólnym (rys. 23, więcej informacji także TUTAJ)
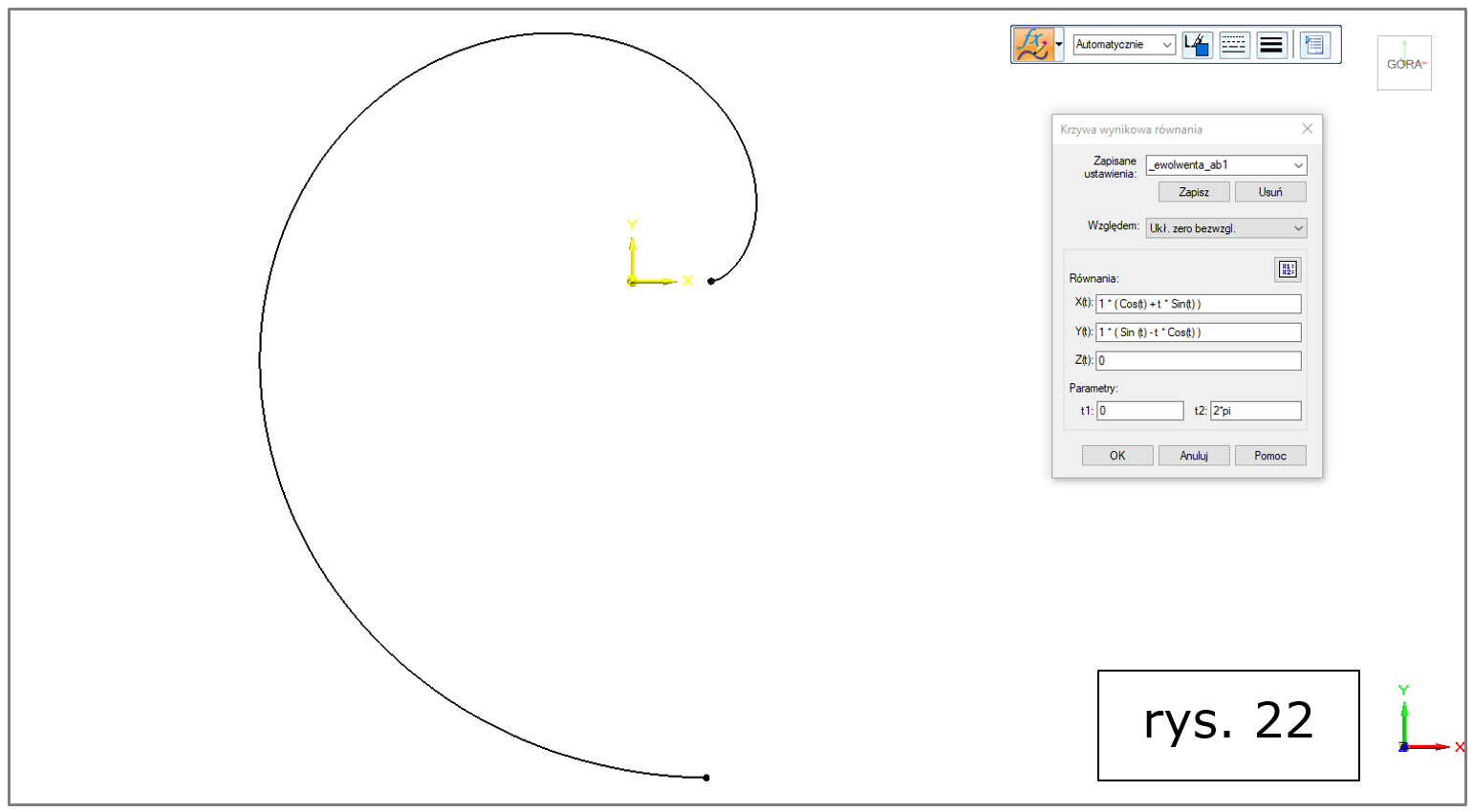
Rys. 22. Solid Edge 2022 – krzywa wynikowa równania, ewolwenta
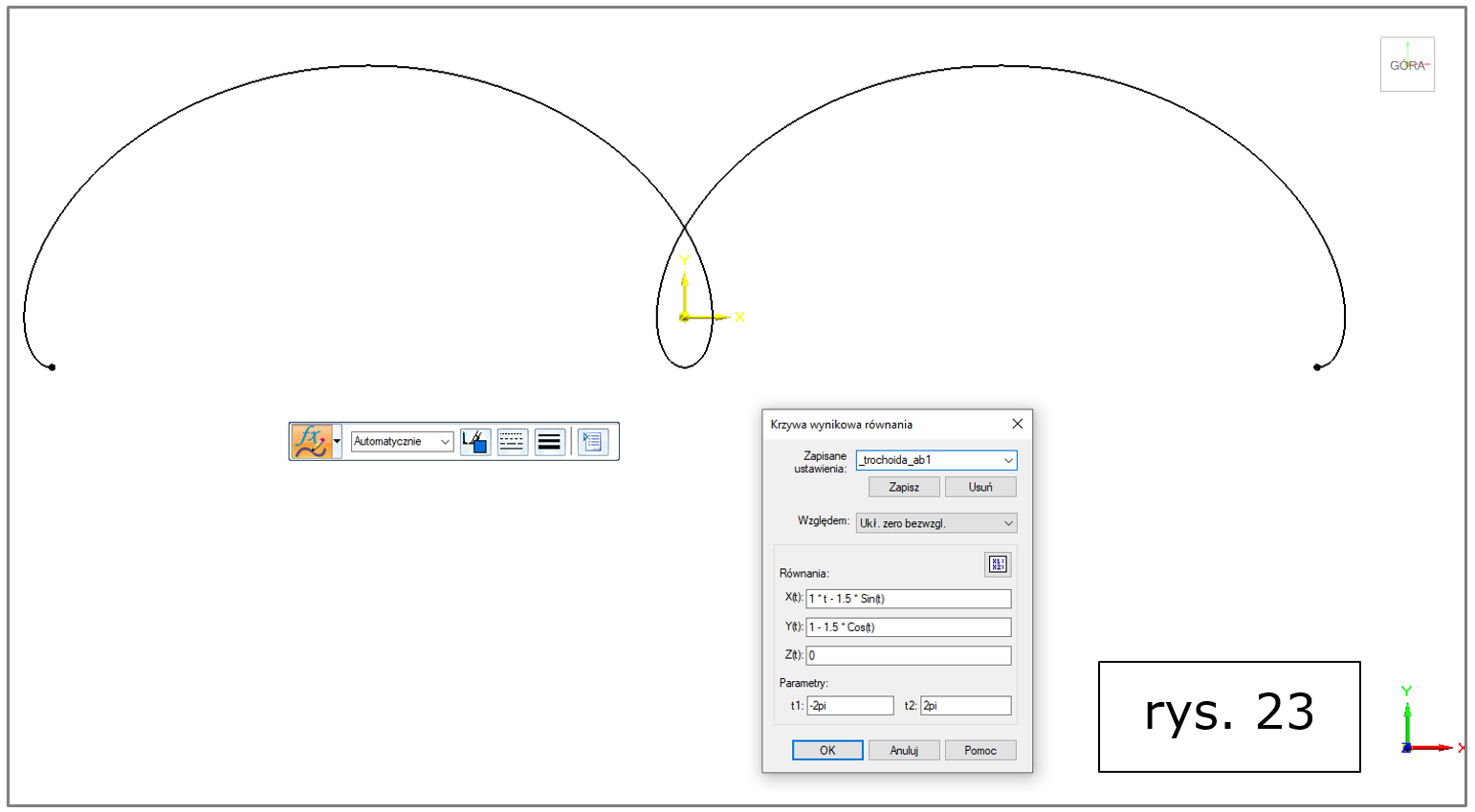
Rys. 23. Solid Edge 2022 – krzywa wynikowa równania, trochoida
– dynamika:
ad f) krzywa Lissajou (rys. 24, więcej informacji także TUTAJ oraz TUTAJ)
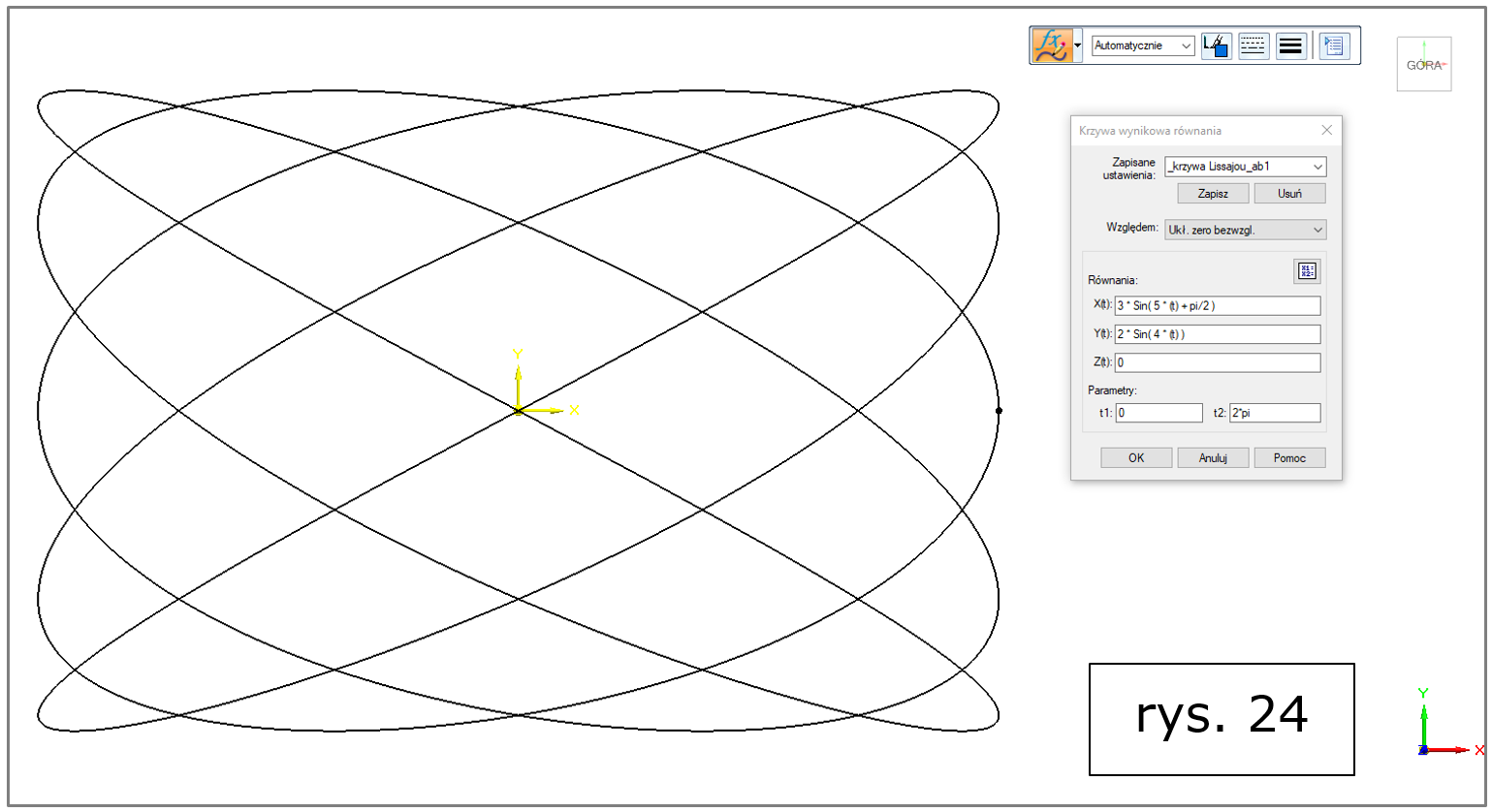
Rys. 24. Solid Edge 2022 – krzywa wynikowa równania, krzywa Lissajou
– energetyka, budownictwo, architektura:
ad g) krzywa łańcuchowa (rys. 25, więcej informacji TUTAJ oraz TUTAJ)
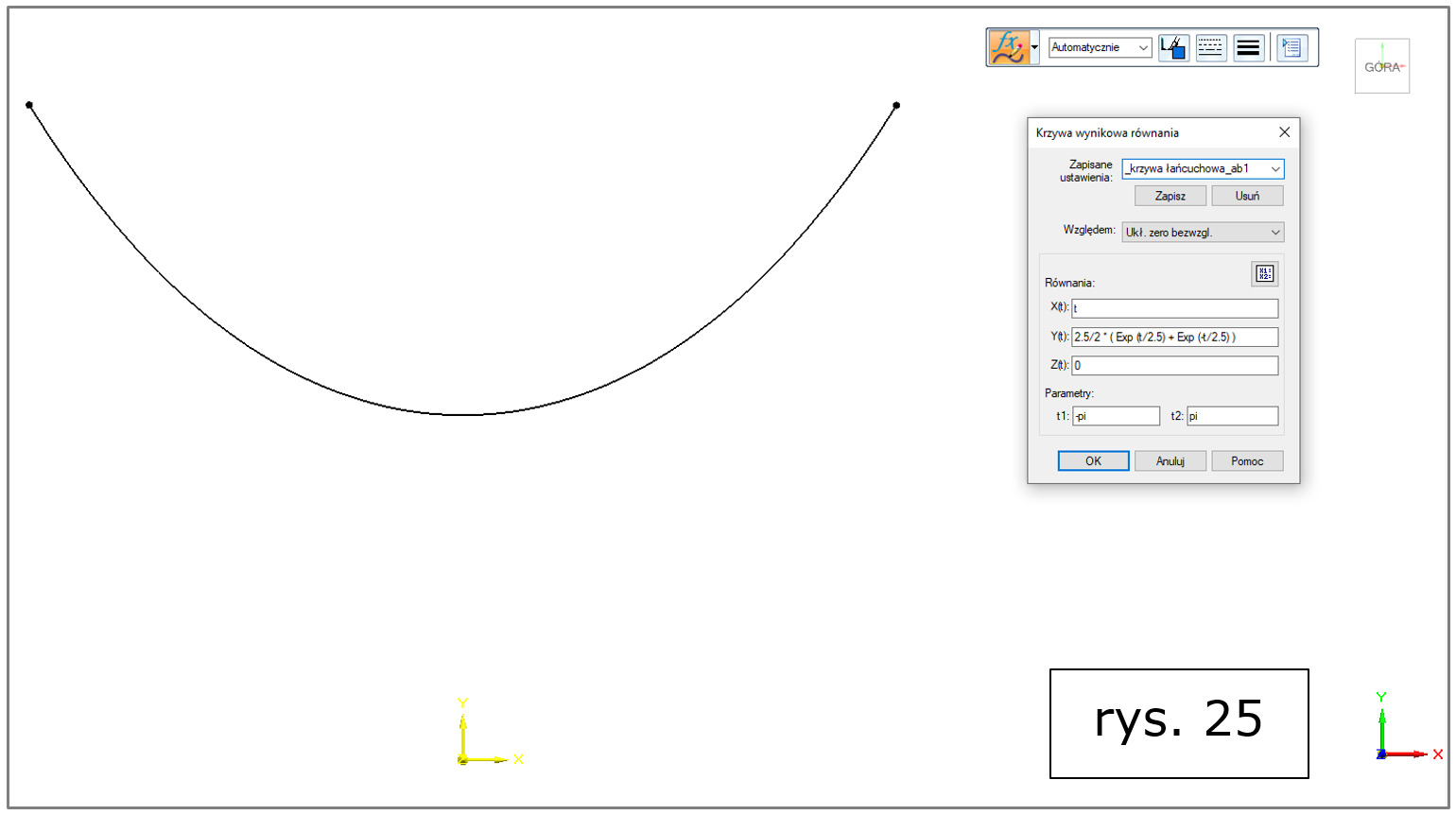
Rys. 25. Solid Edge 2022 – krzywa wynikowa równania, krzywa łańcuchowa
– elektrotechnika:
ad r) spirala Slinky (rys. 26, więcej informacji TUTAJ oraz TUTAJ)
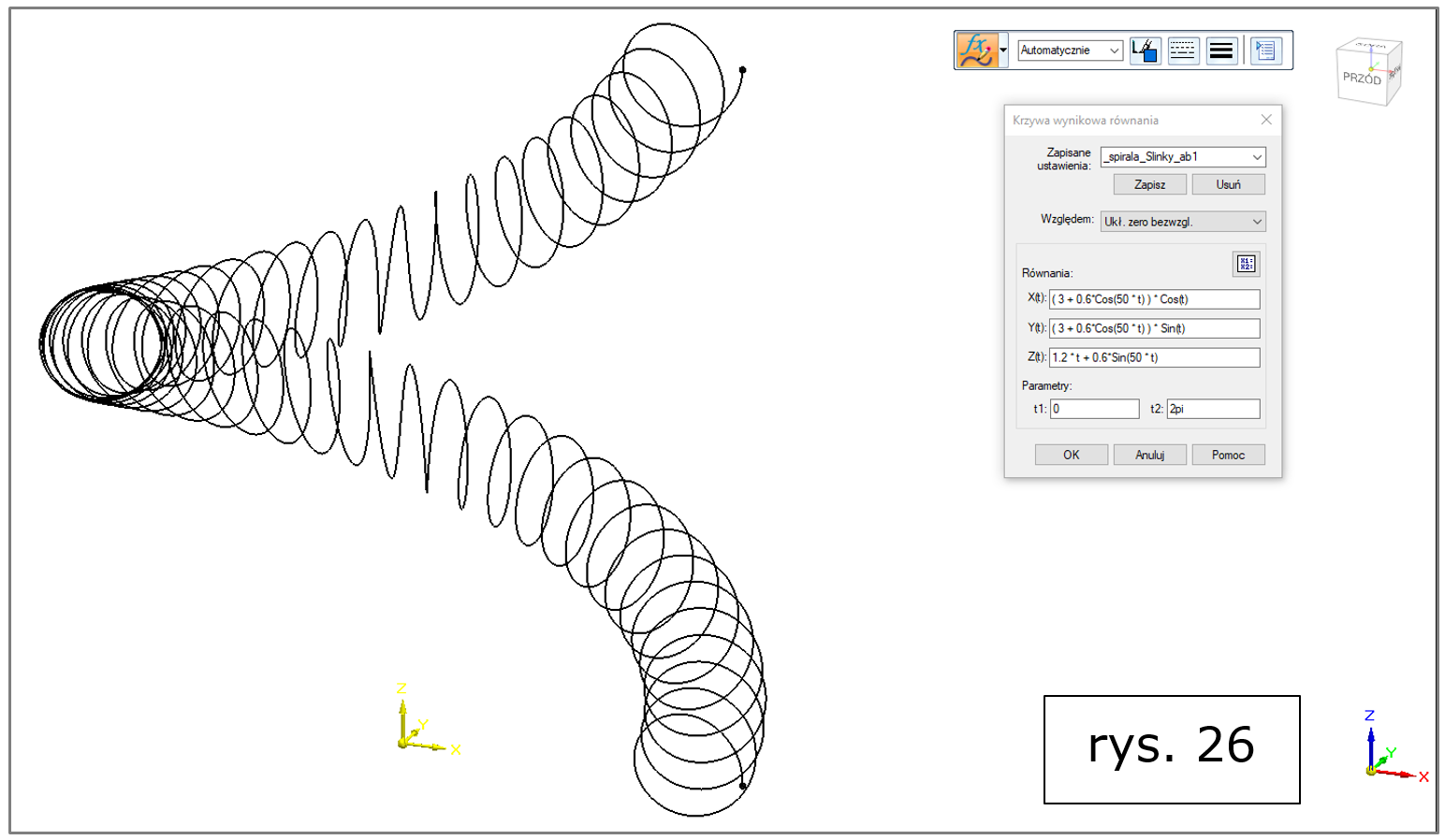
Rys. 26. Solid Edge 2022 – krzywa wynikowa równania, spirala Slinky
Wybrany efekt zastosowania tych poleceń dla modelowania wyrobu z branży wzornictwa przemysłowego przedstawiono na rys. 27.
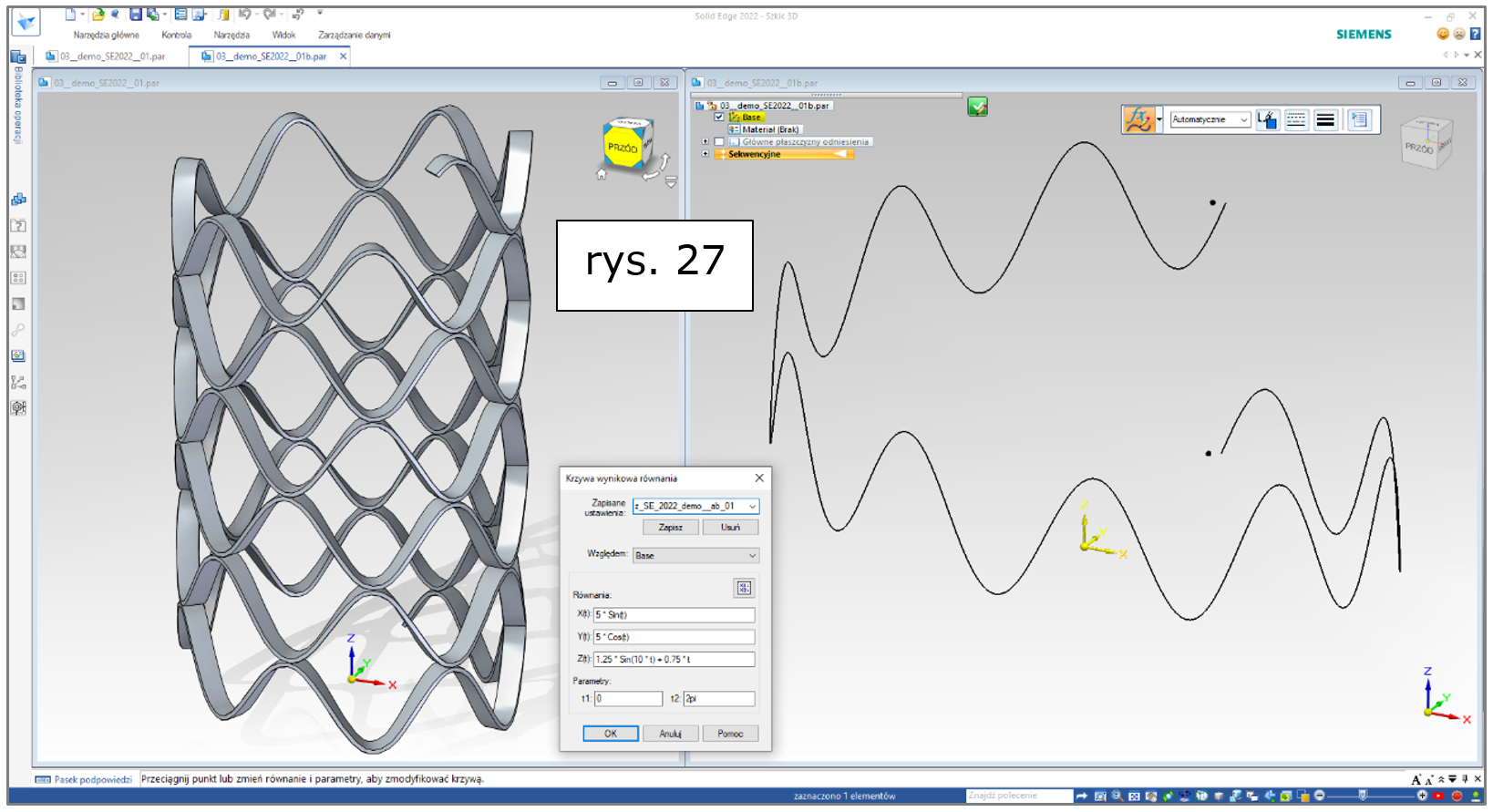
Rys. 27. Solid Edge 2022 – krzywa wynikowa równania, wybrany efekt finalny
Zakończenie
W przypadku opisanych tu nowych rozwiązań SOLID EDGE 2022 dla modelowania powierzchni swobodnych i krzywych parametrycznych, warto wyprowadzić wnioski w dość retoryczny sposób.
Najlepszą oceną dla przedstawionych tu funkcjonalności będzie miara czasu, które duża część użytkowników Solid Edge 2022 może zaoszczędzić, w stosunku do działań prowadzonych uprzednio.
Wstępne szacunki dostarczone przez wczesnych użytkowników podają, iż skrócenie istotnych zadań projektowych może osiągnąć nawet (uśredniając) 50%.
Tak uzyskana znacząca oszczędność czasu podczas prac projektowych to najlepszy wniosek, jaki można tu przedstawić.
c. d. n….
Opracował: dr inż. Adam Budzyński