Weryfikacja metod obliczeniowych MES
Weryfikacja metod obliczeniowych MES jest bardzo ważnym aspektem, który należy rozważyć podczas przeprowadzania obliczeń dla analizowanej konstrukcji. W związku z dużymi kosztami wynikającymi z procesu tworzenia zaawansowanych stoisk badawczych, posłużyć się można prostymi wzorami, które znaleźć można w ogólnie dostępnej literaturze.
Analiza belki
Najprostszym przypadkiem weryfikacji MES jest analiza belki o odpowiednio zdefiniowanym przekroju, która z jednej strony jest usztywniona, czyli mówiąc w uproszczeniu zabetonowana w ścianę, a na drugim końcu obciążona siłą. Przypadek ten może dokładnie zobrazować poprawność przeprowadzonych obliczeń. Dodatkowo posiłkując się różnymi elementami dostępnymi z poziomu metody elementów skończonych, możemy zobaczyć różnicę w wynikach pomiędzy poszczególnymi elementami, takimi jak elementy 1D, 2D oraz 3D. Przedmiotem analizy była belka o przekroju dwuteowym (Rys. 1), ze względu na dość częste wykorzystywanie tego typu elementu w różnych konstrukcjach.
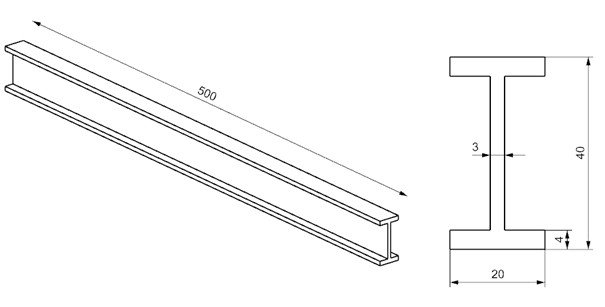
Obliczenia MES, jak wspomniałem wcześnie,j przeprowadzono wykorzystując różne typy elementów (belkowe 1D, powłokowe 2D, bryłowe 3D – czworościenne oraz sześciościenne), co dało nam 4 modele obliczeniowe rys 2 – 3.

Posługując się prostymi wzorami analitycznymi, możemy otrzymać wartości przemieszczeń, które następnie możemy porównać do obliczeń MES (tabela 1). W tabeli uwzględnioną również wartość procentową błędu, dla której wartością referencyjną była wartość obliczona metodą analityczną.
– przemieszczenie względne końca belki
P – siła
L – długość belki
E – moduł Younga
J – moment bezwładności przekroju
Tabela 1 Wartości przemieszczeń dla 4 modeli MES i dla modelu analitycznego.
| Model belkowy 1D | Model powierzchniowy 2D | Model 3D (Hexa) | Model 3D (Tetra) | Metoda analityczna | |
| Liczba elementów | 40 | 4008 | 6513 | 191320 | – |
| Przemieszczenia | 3,518 | 3,334 | 3,515 | 3,518 | 3,458 |
| Błąd wyników [%] | -1,753 | 3,586 | -1,648 | -1,753 | – |
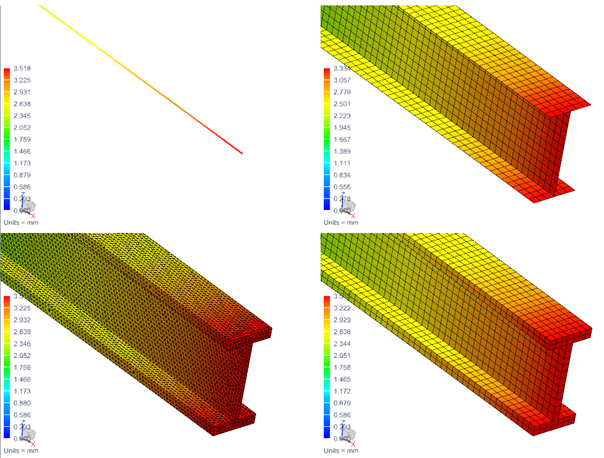
Wyniki uznaje się za poprawne, jeśli mieszczą jest w przedziale nie większym niż 5%. Wszystkie wyniki spełniają ten warunek. Najdokładniejszy wynik otrzymaliśmy używając elementów 3D sześciościennych. W elementach belkowych często zdarza się, że błąd obliczeń jest bardzo mały lub niewielki, im dłuższa jest długość belki. Nie powinno się używać elementów belkowych dla obiektów o małej długości analizowanego obiektu. Na rys. 4 przedstawiono wartości przemieszczeń dla wszystkich 4 analizowanych przypadków.
Analiza konstrukcji ramowej
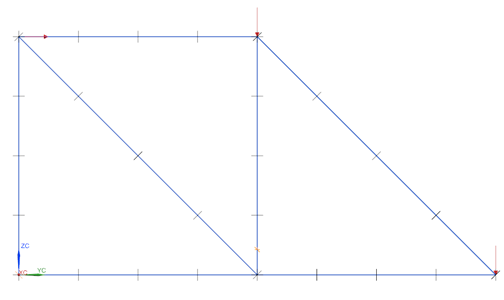
Innym z często spotykanych przypadków weryfikacji metod obliczeniowych MES jest wyznaczenie sił w konstrukcjach prętowych. Rysunek poglądowy przedstawiono na rys. 5.
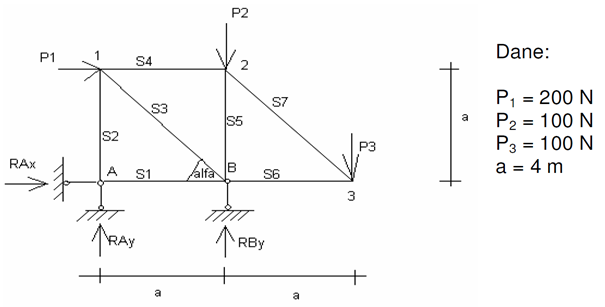
W celu wyznaczenia sił w poszczególnych prętach w pierwszej kolejności wyznaczono reakcję podpór na kierunku X i Y. W dalszej kolejności wyznaczono siły w prętach przy użyciu metody analitycznej przeznaczonej głownie dla kratownic, zwana metodą równania węzłów. Polega ona na przyrównywaniu do zera rzutów wszystkich sił działających na każdy węzeł.
Model MES zbudowany z elementów prętowych 1D przedstawiono na rys. 6. Ważnym aspektem jest podkreślenie typu zastosowanego elementu 1D; mam tu na myśli element prętowy, ponieważ wybór tego elementu będzie wpływał na końcowe wyniki obliczeń, a dokładniej na wartości sił.
W poprzednim przykładzie zastosowano elementy belkowe 1D. Pamiętaj, że elementy prętowe pracują tylko na rozciąganie oraz ściskanie, natomiast elementy belkowe dodatkowo mają możliwość przenoszenia zginania. W przypadku obliczeń konstrukcji kratownicowych, dla których potrzebujemy uzyskać wartości sił w prętach, słuszniejsze będzie zastosowanie elementów prętowych. Wartości wyliczonych sił wyświetlono w formie graficznej przy zastosowaniu elementu prętowego przedstawiono na rys. 7.

Wyniki sił dla przykładowych prętów, wyliczony metodą analityczną oraz metodą MES przedstawiono w tabeli 2. Zauważ, że w tabeli uwzględniono również wartości sił przeliczone również przy zastosowaniu elementu belkowego.
Tabela 2. Porównawcza wyników obliczeń sił dla analizowanej kratownicy.
| Wartość siły [N] | |||
| MES (Belkowe) | MES (Prętowe) | Analityczne | |
| S1 | 198,433 | 199,956 | 200 |
| S3 | 420,65 | 422,869 | 424,33 |
| S6 | -99,405 | -99,749 | -100 |
Drgania własne
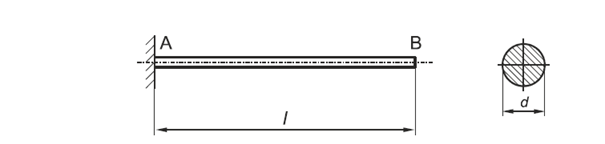
Ostatnim przykładem, który chcę przedstawić, jest możliwość weryfikacji obliczeń MES również na przykładzie częstotliwości drgań własnych konstrukcji. Do przedstawienia tego przykładu wykorzystano prostą belkę utwierdzoną na jednym końcu rys. 8.
Wzór, który wykorzystano do obliczeń postaci drgań własnych metodą analityczną przedstawiono poniżej:
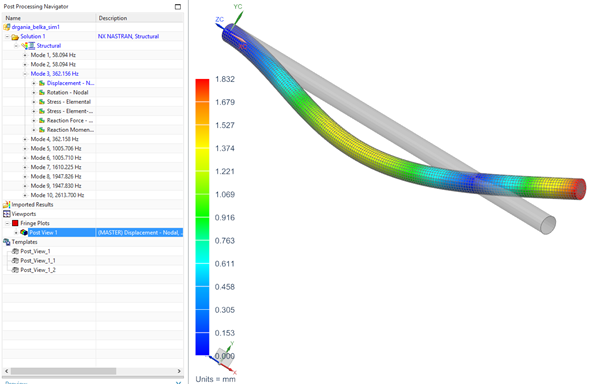
Model MES analizowanego obiektu składał się z elementów 3D (sześciościennych), rys. 9. Dodatkowo na jednym końcu obiektu usztywniono go, odbierając możliwość przemieszczania się jak również rotacji.

Wyniki obliczeń pierwszych 4 postaci drgań własnych wraz z konturami przemieszeń dla postaci 3 przedstawiono na rys. 10.
Wyniki obliczeń postaci drgań własnych metodą analityczną oraz metodą MES przedstawiono w tabeli 3.
Tabela 3. Porównanie wyników postaci częstotliwości drgań wraz z wynikami analitycznymi.
| Postać 1 | Postać 2 | Postać 3 | Postać 4 | |
| Metoda analityczna [Hz] | 58,44 | 366,27 | 1025,40 | 2009,79 |
| Metoda MES [Hz] | 58,094 | 362,156 | 1005,76 | 1947,826 |
| Błąd [%] | 0,59% | 1,12% | 1,92% | 3,08% |
Podsumowanie
Weryfikację metod obliczeń MES przy użyciu uproszczonych wzorów można wykorzystać nie tylko w obliczeniach statycznych czy drgań; często modele belkowe wykorzystywane są do obliczeń wyboczenia w celu określenia siły krytycznej, przy której nastąpi utrata stateczności pręta, a następnie może dojść do zerwania. W sieci można znaleźć wiele różnych publikacji, w których autorzy przedstawiających obliczenia MES oraz jej weryfikację na podstawie rzeczywistych testów, jak również przy użyciu prostych lub bardziej skomplikowanych metod analitycznych. W różnych gałęziach przemysłu np. w lotnictwie, pewne części lotnicze (takie jak np. łopatki turbin, sprężarek, koła zębate, wały) analizowane są przy użyciu sprawdzonych metodyk modelowania, przez co nie wymagają przeprowadzania rzeczywistych testów, a wyniki analiz MES są akceptowane przez FAA (Federal Aviation Administration).
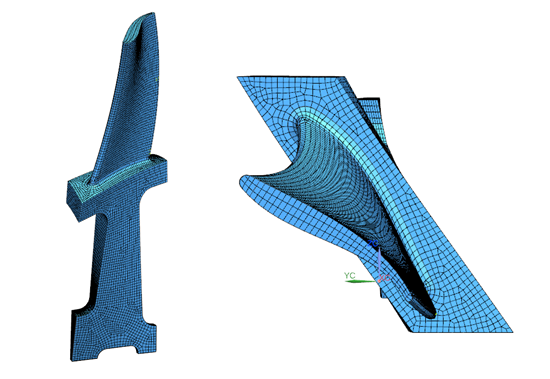
Wspominam o różnych metodykach, ponieważ model musi spełniać pewne kryteria tzn. musi zostać podzielony w taki sposób, aby można było nałożyć na niego tylko i wyłącznie elementy sześciościenne. Dodatkowo dochodzą do tego oczywiście inne kryteria, jak poprawne zadanie warunków brzegowych, obciążeń itp. Tylko w taki sposób przygotowane siatki obliczeniowe rys. 11 – 12 są dopuszczone do obliczeń w przypadku przemysłu lotniczego.

Artykuł ten stanowi drugą część cyklu edukacyjnego poświęconego tematyce MES i miał na celu zapoznać czytelników z zaletami stosowania metody elementów skończonych. W ramach wspomnianej akcji przedstawimy możliwości modelowania procesu MES na podstawie wybranych bloków tematycznych. Każdy kolejno opublikowany materiał będzie posiadał własny film podsumowujący przedstawione zagadnienie. Zapraszamy do śledzenia naszego bloga oraz kanałów społecznościowych, gdzie będziemy informować o kolejnych materiałach i wydarzeniach związanych z tym cyklem.
Poniżej znajduje się nagranie webinaru na temat „NX CAE – wielofunkcyjne środowisko MES”
opracował
Marek Rudy
marek.rudy@gmsystem.pl
