Optymalizacja wielokryterialna typu Pareto: środowisko HEEDS Siemens
W wielu gałęziach przemysłu musimy sobie radzić z zwiększeniem produkcji i złożonością procesów produkcyjnych. W związku z potrzebą skrócenia procesu rozwoju produktu, zrównoważonym rozwojem i niższymi kosztami, osiągnięcie innowacyjności jest bardzo trudne. Naprzeciw tym oczekiwaniom wychodzi środowisko HEEDS.
Wstęp
HEEDS automatyzuje i przyspiesza proces przeszukiwania rozwiązań w przestrzeni projektowej. Oprogramowanie to umożliwia optymalizację geometrii na bazie wyznaczonych kryteriów, tak aby spełnić wymagania klienta (projektanta).
Dzięki środowisku HEEDS odkrywa się szybsze i lepsze projektowanie. Środowisko HEEDS zapewnia:
- Automatyzację procesu (automatyczne tworzenie wirtualnego prototypu)
- Rozproszone wykonanie (przyspieszone testowanie wirtualnego prototypu)
- Efektywne przeszukiwanie (poszukiwanie lepszych alternatyw projektowych)
- Przegląd i odkrywanie (zapewnienie rzetelnych osiągów produktu)
W poniższym artykule przedstawiona została optymalizacja rurki należąca do silnika spalinowego ciężarówki. Ta optymalizacja została wykonana dzięki środowisku HEEDS. W tym celu potrzebne było przygotowanie analizy CFD w środowisku STAR CCM+ pod kątem minimalizacji wirów oraz otrzymania jednolitego rozkładu prędkości na wylocie z rury. Dodatkowo wymagane było wykonanie parametrycznego modelu w środowisku CAD.HEEDS pozwala na wielokryterialną optymalizację wielu środowisk projektowo – obliczeniowych dzięki otwartej platformie umożliwiającej spinanie ze sobą dowolnego środowiska CAD z dowolnym solwerem obliczeniowym (FEM/CFD) i nie tylko. Na rys.1 przedstawiono szeroką paletę systemów CAD/CAE/CFD, które mogą być ze sobą łączone w środowisku HEEDS.
Rys.1 Lista dostępnych systemów do połączenia ze sobą w środowisku HEEDS
Wymiana danych w środowisku HEEDS odbywa się poprzez użycie prostego schematu blokowego, który pozwala na wymianę danych wejściowych i wyjściowych pomiędzy wybranymi systemami, co zostanie przedstawione w dalszej części artykułu.
Przygotowanie parametrycznej geometrii CAD
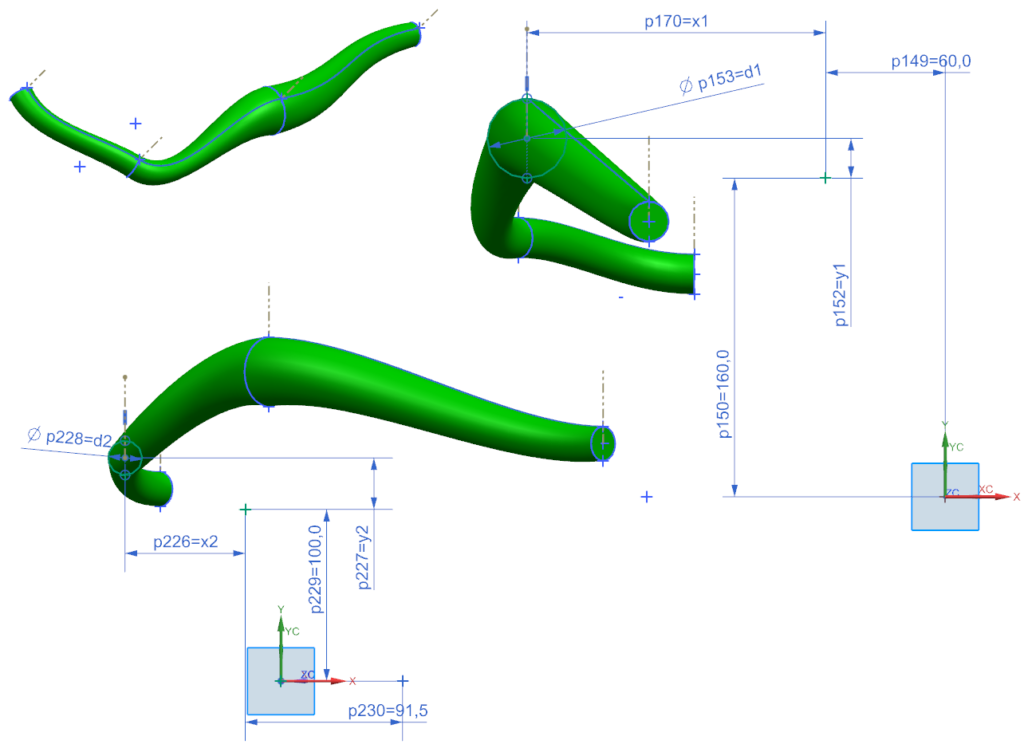
Przygotowana parametryczna geometria CAD rurki wykonana zostało w środowisku NX CAD. Do dyspozycji mamy wiele zmiennych, które określają kształt końcowy rurki. Do optymalizacji wykorzystano 7 zmiennych X1, X2, Y1, Y2, R1, R2 oraz kąt pochylenia płaszczyzny, na której znajduje się szkic środkowy rurki (rys.2).
Rys.2 Parametryczny model rurki oraz 7 zmiennych, które posłużą do jej optymalizacji
Analiza przepływu w środowisku STAR CCM +
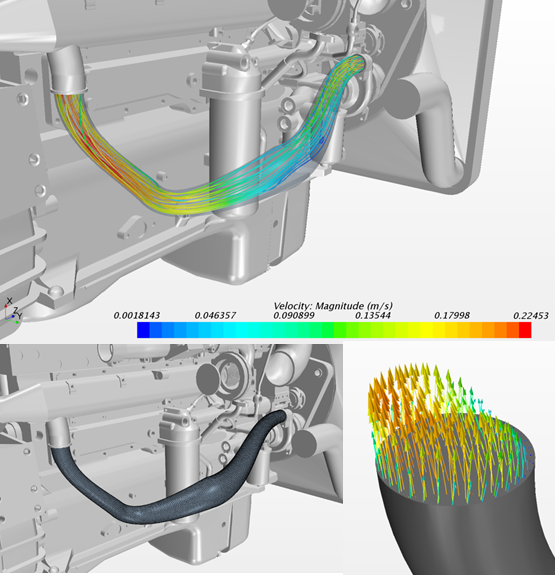
Drugim krokiem było przygotowanie obliczeń CFD w środowisku STAR CCM +. Zanim przejdziemy do procesu optymalizacji, musimy w środowisku przygotować bazową analizę przepływową (rys.3), która będzie plikiem wsadowym do środowiska HEEDS. W analizie CFD zdeklarowano dwa parametry, które posłużą nam jako pewne kryteria w dalszym procesie optymalizacji. Parametrami tymi było:
- Zawirowanie przepływu na wylocie
- Równomierność przepływu
Rys.3 Przygotowanie analizy przepływu w środowisku STAR CCM +
Optymalizacja w środowisku HEEDS
Trzecim krokiem, a zarazem najbardziej kluczowym, jest spięcie ze sobą oprogramowania NX CAD oraz STAR CCM+ poprzez automatyzację, wymianę danych pomiędzy systemami i przeprowadzenie optymalizacji przy użyciu algorytmu SHERPA na bazie wielokryterialnej metody typu Pareto. Dodatkowo HEEDS oprócz metody SHERPA zapewnia inne możliwe algorytmy optymalizacji takie jak:
MO-SHERPA – MULTI–objective optimization
DOE – Design of Experiments
R&R – Reliability and Robustness
RSM – Response Surface Method
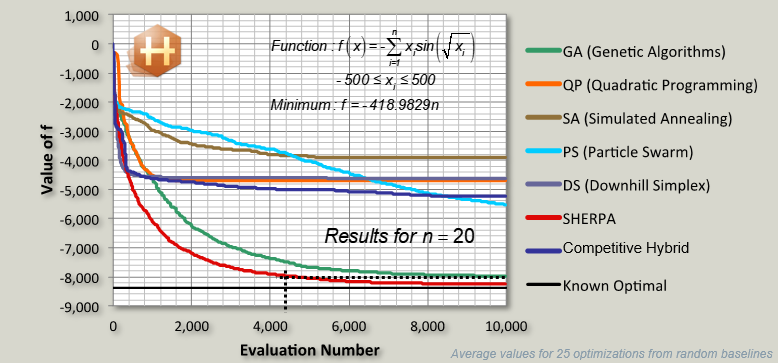
Design SweepPoniżej przedstawiono przykład wykorzystania algorytmu SHERPA zastosowanego do znalezienia minimalnej wartość funkcji przy najmniejszej liczbie próbkowania oraz porównanie go z innymi algorytmami dostępnymi na rynku (rys. 4). Jak widać na rys. 4. wystarczyło wykonanie już 2000 próbkowań, aby znaleźć optymalne minimum. SHERPA wykonał >10% szybciej niż każdy inny algorytm i >30% lepiej niż algorytm hybrydowy. Algorytm SHERPA bazuje na połączeniu wszystkich zalet dla metodyki hybrydowej oraz adaptacyjnej.
Rys. 4 Wyznaczenie minimum funkcji dla różnych algorytmów
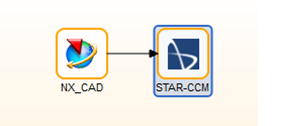
Wróćmy do ustawienia odpowiednich bloków odpowiadających danemu oprogramowaniu w środowisku HEEDS oraz spięciu ich ze sobą wraz z wymianą danych wejściowych i wyjściowych (rys. 5-7).
Rys.5 Schemat blokowy łączenia systemów w środowisku HEEDS
Rys. 6 Pliki wejściowe dla środowiska HEEDS
Rys.7 Pliki wyjściowe dla środowiska HEEDS
Kluczowym aspektem w procesie optymalizacji w środowisku HEEDS jest również wyznaczenie zakresu przeszukiwania parametrów obliczeniowych tak, aby system wiedział w jakim zakresie może przeszukiwać naszą geometrię (rys. 8).
Rys.8 Zakres przeszukiwania parametrów w środowisku HEEDS
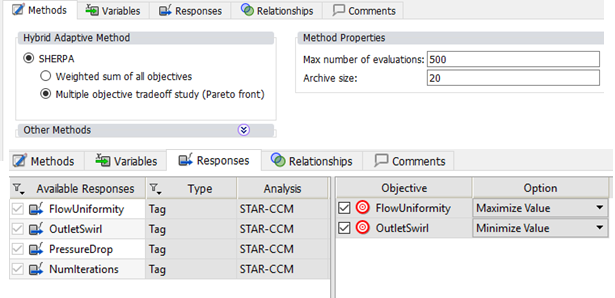
Końcowym etapem jest ustawienie metody optymalizacji typu Pareto. Wyjaśnijmy sobie w kilku zdaniach, czym jest metoda Pareto. Mając dany zbiór możliwych rozwiązań danego zagadnienia i sposób ich oceny, możemy wyznaczyć tzw. front Pareta (nazywany także zbiorem Pareta), czyli zbiór rozwiązań optymalnych w sensie Pareta. Poprzez ograniczenie zbioru wszystkich możliwych rozwiązań do podzbioru rozwiązań Pareta optymalnych, wybór końcowego rozwiązania przez osobę decydującą ograniczony jest do tego podzbioru, co ułatwia podjęcie decyzji .
Rys. 9. Wykres frontu Pareto
Rys. 10 Definiowanie metody optymalizacji oraz ustawiania kryteriów dla algorytmu obliczeniowego
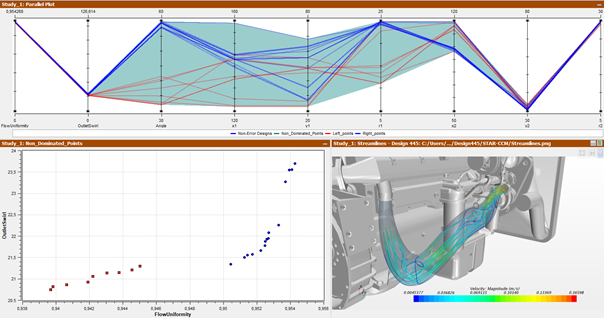
Ostatnim etapem jest post- procesing, czyli wyodrębnienie najlepszego kandydata. Odbywa się to dzięki intuicyjnemu interfejsowi graficznemu, który pokazuje w formie prostych wykresów parametry, które miały największy i najmniejszy wpływ na naszą optymalizację wraz z przykładowym rozkładem graficznym prędkości w rurce.
Rys. 11 Rozkład graficzny prędkości wraz z wykresem parametrów i ich wpływ na optymalizację w środowisku HEEDS
Dzięki zastosowaniu środowiska HEEDS jesteśmy w stanie bardzo szybko znaleźć satysfakcjonujące rezultaty optymalizacji. Środowisko to pozwala skupić się na wyborze najlepszego wariantu projektu, nie na wirtualnym procesie testowania.HEEDS wykonuje optymalizację niezależnie od złożoności i ilości parametrów. Wystarczy tylko określić czas oraz liczbę przeszukiwania modelu, jaki system ma poświęcić, aby otrzymać odpowiedź, a algorytm SHERPA inteligentnie dostosowuje strategię przeszukiwania w celu znalezienia najlepszego rozwiązania tak jak to zrobił dla naszej rurki (rys. 12).
Rys. 12. Rozkład graficzny prędkości na wylocie z rury oraz kształt rurki przed i po procesie optymalizacji.
http://www.redcedartech.com/pdfs/SHERPA.pdf
https://pl.wikipedia.org/wiki/Optimum_w_sensie_Pareto
Opracował: Marek Rudy