W poszukiwaniu projektu idealnego, czyli przykłady zastosowań modelowania parametrycznego oraz optymalizacji CAD w systemie 3D/2D Solid Edge
1. Wstęp – celowość stosowania modelowania parametrycznego we współczesnej branży CAD
W pracy przedstawiono wybrane przykłady modelowania parametrycznego w branży mechanicznej, możliwego do zaistnienia dzięki wykorzystaniu nowoczesnych rozwiązań CAD 3D/2D (na przykładzie systemu SIEMENS https://gmsystem.pl/solid-edge/).
Modelowanie parametryczne jest jedną z metod prowadzenia zaawansowanych prac projektowych, polegającą na tym, iż w geometrycznym modelu wybranego produktu wyróżnia oraz charakteryzuje się istotne wielkości zmienne.
Odpowiednia zmiana wartości dla tak wybranych zmiennych umożliwia zarządzanie kluczowymi aspektami geometrii omawianego numerycznego zapisu konstrukcji, tj. szybką modyfikację jego postaci ze stanu początkowego do odgórnie zamierzonego stanu docelowego.
W ogólnym rozumieniu, w modelach CAD rozróżnia się 3 rodzaje zmiennych:
a) zmienne wymiarowe, np. wartości wymiarów długości i kąta (wartości nominalne z ew. odchyłkami),
– w pojedynczych komponentach: wybrane gabaryty części / części blaszanych,
– w złożeniach: odległości pomiędzy poszczególnymi częściami (zadane, minimalne, maksymalne, itd.),
b) zmienne skalarne, np. liczby wystąpień poszczególnych obiektów:
– w pojedynczych komponentach: liczność poszczególnych operacji (otworów, rowków, „kieszeni”, itd.) powielonych z zastosowaniem szyków,
– w złożeniach: liczba sztuk poszczególnych komponentów, także możliwych do namnożenia za pomocą różnorodnych szyków,
c) zmienne logiczne, np. fakt występowania / lub nie, ww. obiektów w projekcie:
– w pojedynczych komponentach: zablokowanie wykonania określonej operacji,
– w złożeniach: zablokowanie występowania komponentu w złożeniu.
Wprowadzając zamierzone zmiany do wybranej grupy ww. zmiennych, model danego wyrobu ulega szybkiej transformacji do postaci modelu innego wyrobu, różniącego się od oryginału pod konkretnymi względami geometrycznymi.
W ten sposób uzyskuje się wielo-wariantowość konstrukcji CAD.
Dodatkowe zastosowanie arkusza kalkulacyjnego MICROSOFT EXCEL do zarządzania zbiorami wartości ww. zmiennych (uporządkowanymi do postaci baz danych), a także do właściwego i szybkiego eksportu tych wartości do systemu CAD w ww. celu, dodatkowo zwiększa zakres zautomatyzowania przedsięwzięcia.
W pracy przedstawiono także przykłady zautomatyzowanej optymalizacji tak uzyskanych „wysoce parametrycznych” modeli 3D, pod uprzednio sprecyzowanym względem.
2. Przykłady produktów, oferowanych na rynku w różnych wersjach, podobnych pod względem geometrycznym.
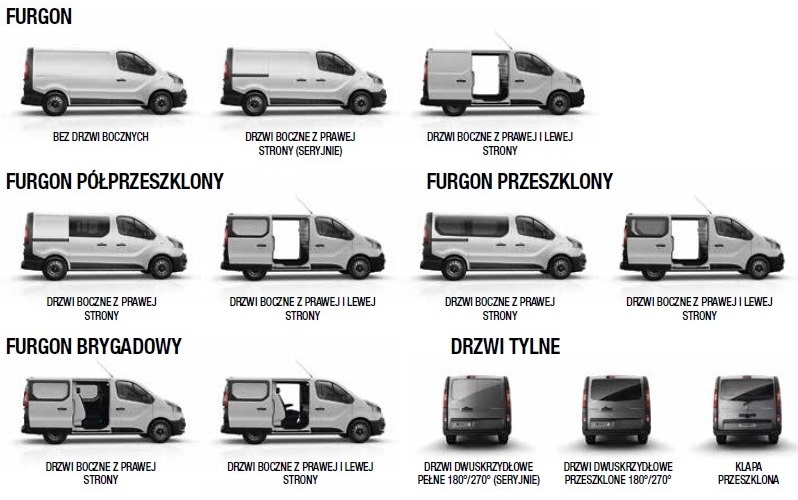
Branża motoryzacyjna charakteryzuje się adresowaniem ogólnie rozumianego produktu do zróżnicowanych odbiorców docelowych. Przykładem są chociażby różnorodne wersje konfiguracji / wyposażenia danego pojazdu, w zależności od możliwości nabywczych oraz upodobań klientów końcowych, co – na przykładzie zróżnicowanych wersji nadwoziowych danego samochodu – przedstawiono na rys. 2.1., a wariantów kokpitu kierowcy w zależności od wersji auta, na rys. 2.2.
Zważywszy, iż ogólnodostępne dziś profesjonalne systemy CAD wywodzą się głównie z przemysłu obronnego, lotniczego i samochodowego (i głównie na bazie ‘tamtejszych wyzwań’ są one rozwijane), wręcz pewne jest, iż renomowani producenci przedstawionych tu aut zastosowali modelowanie parametryczne dla szybkiego uzyskania wielu wariantów geometrycznych oferowanego wyrobu. Jest to zapewne spowodowane potrzebą możliwie szybkiego tworzenia i aktualizowania oferty rynkowej
w warunkach tzw. agresywnej konkurencji (auta obecnie mają swe „premiery” od razu w znaczącej większości oferowanych wersji).
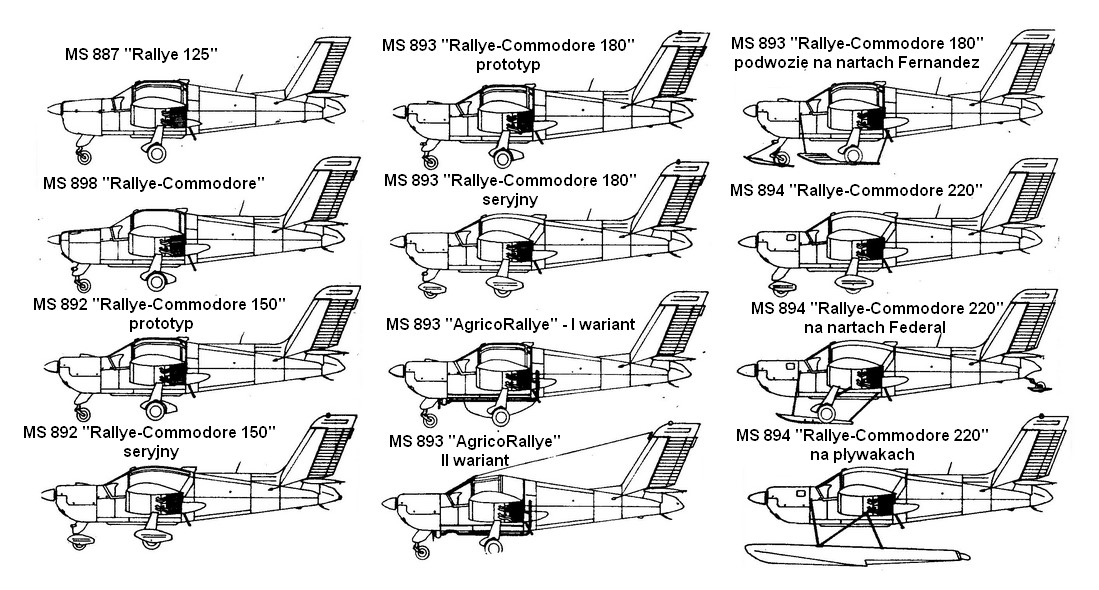
Dla kontrastu, na rys. 2.3. przedstawiono wybrane wersje samolotu Morane-Saulnier/SOCATA Rallye (produkowanego też w Polsce pod nazwą PZL-110 Koliber). Znamiennym jest, iż został on opracowany w latach 50. XX wieku, więc (z racji znanej dekady rozpowszechnienia się profesjonalnych rozwiązań CAD na rynku cywilnym) bez wykorzystania modelowania parametrycznego. Widoczne tu odmienne wersje tego samolotu opracowywane były w odstępie aż od kilku- do kilkunastu miesięcy. Widać więc znaczący postęp, jaki ‘niesie ze sobą’ stosowanie modelowania parametrycznego CAD.

3. Konfigurator produktu, jako docelowy efekt zastosowania modelowania parametrycznego.
3.1 Przykład z branży publicznego transportu szynowego (kokpit, in. pulpit motorniczego tramwaju).
Analogicznie do przykładu z rys. 2.2, pulpity różnych odmian danego pojazdu szynowego, oferowanego przez konkretnego producenta też mogą się od różnić i często tak właśnie jest w praktyce. Wybrany wariant ww. pulpitu, do zabudowy w danej wersji tramwaju typu JAZZ, produkcji firmy PESA Bydgoszcz S.A. przedstawiono na rys. 3.1.1.

Powyższa różnorodność wynika z faktu, iż wyrób końcowy ma spełniać szereg wymagań zapisanych
w ‘Specyfikacji Istotnych Warunków Zamówienia’ (‘SIWZ’, rys. 3.1.2). Gdy klient (np. Miejskie Zakłady Komunikacji w Toruniu Sp. z o.o., Tramwaje Warszawskie Sp. z o.o. lub Miasto Łódź, itd.) sprecyzuje głównie następujące kwestie:
– infrastruktura miasta lub jego rejonów, po którym ma docelowo poruszać się pojazd,
– rodzaj zastosowanego systemu informacji pasażerskiej,
– rodzaj wyposażenia multimedialnego pojazdu,
wówczas wynika z tego szereg wytycznych, wpływających na geometrię omawianego pulpitu. Należą do nich m.in.:
– tryb jazdy tramwaju (jednokierunkowy lub dwukierunkowy),
– rozmiar wyświetlacza systemu monitoringu,
– rodzaj rampy dla osób niepełnosprawnych,
– zastosowanie systemu rozgłoszeniowego.
Pod uwagę bierze się także zagadnienia, które nie muszą być ujęte w ‘SIWZ’, lecz wciąż są istotne, np.:
– opcje rozmieszczenia komponentów pulpitu,
– masa całego podzespołu.

Aby skrócić czas trwania procesu konstrukcyjnego (i w konsekwencji produkcyjnego), zwiększając tym samym rentowność przedsięwzięcia, proponuje się niniejszym zainicjowanie wówczas procesu parametrycznego modelowania CAD z uwzględnieniem następujących założeń:
– najistotniejsze wymagania klienta, implikujące parametryczne kształtowanie geometrii modelu pulpitu zestawia się w tabeli, zbudowanej w arkuszu kalkulacyjnym MICROSOFT (MS) EXCEL,
– konkretny wybór dokonany wówczas przez klienta ‘na papierze’ będzie następnie implikował dokonanie analogicznego właściwego wyboru w pliku .XLSX, w wykonaniu upoważnionego konstruktora,
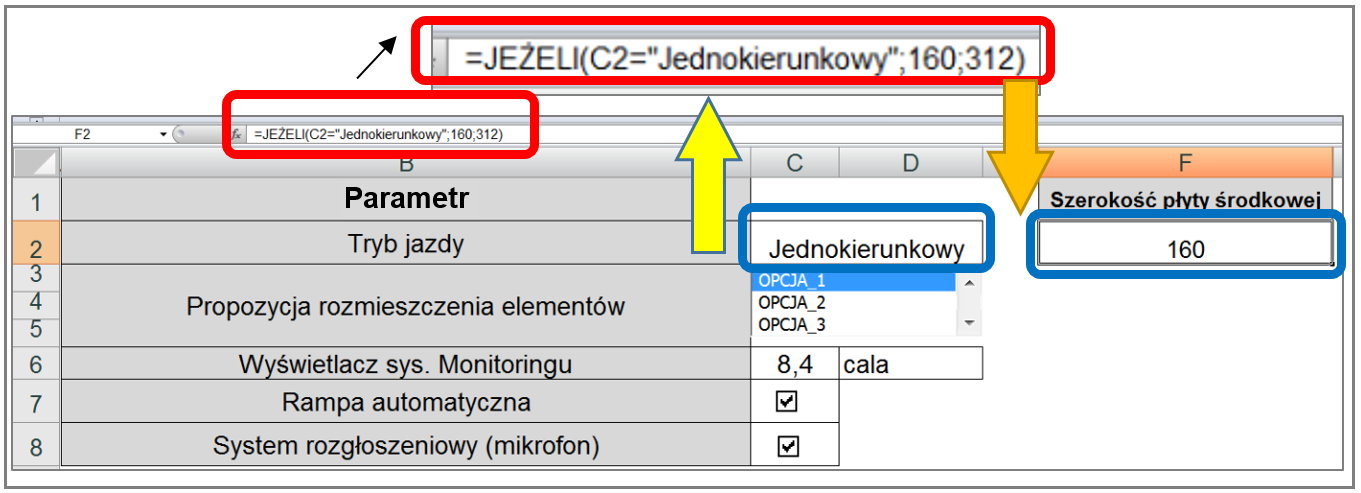
– konsekwencją powyższego będzie wygenerowanie w arkuszu właściwych wartości dla istotnych parametrów opisujących geometrię wyrobu (rys. 3.1.3); mogą one zostać:
• odfiltrowane
• wyszukane wsród uprzednio zdefiniowanych wartości
• obliczone na podstawie przygotowanych formuł,
– tak przypisane wartości konkretnych zmiennych zostają wyeksportowane z arkusza EXCEL do systemu CAD (SIEMENS SOLID EDGE) w wyniku uprzedniego ustanowienia hiperłączy (automatycznie aktualizowanych ‘linków’, pomiędzy wartościami widniejącymi w konkretnych komórkach arkusza EXCEL, a wartościami odpowiednich parametrów geometrycznych, zestawionymi w tzw. ‘tabeli zmiennych’ systemu CAD (rys. 3.1.4),
– początkowa postać geometryczna modelu pulpitu ulega szybkiej i zamierzonej transformacji do tak zdefiniowanej postaci oczekiwanej, z jednoczesną eliminacją błędów projektowych możliwych do popełnienia podczas tworzenia modelu ‘od początku’,
– powyższy korzystny efekt umożliwia relatywnie szybszą finalizację kompletnego procesu produkcyjnego, oznaczając ‘ukoronowanie’ prezentowanej idei zastosowania modelowania parametrycznego.
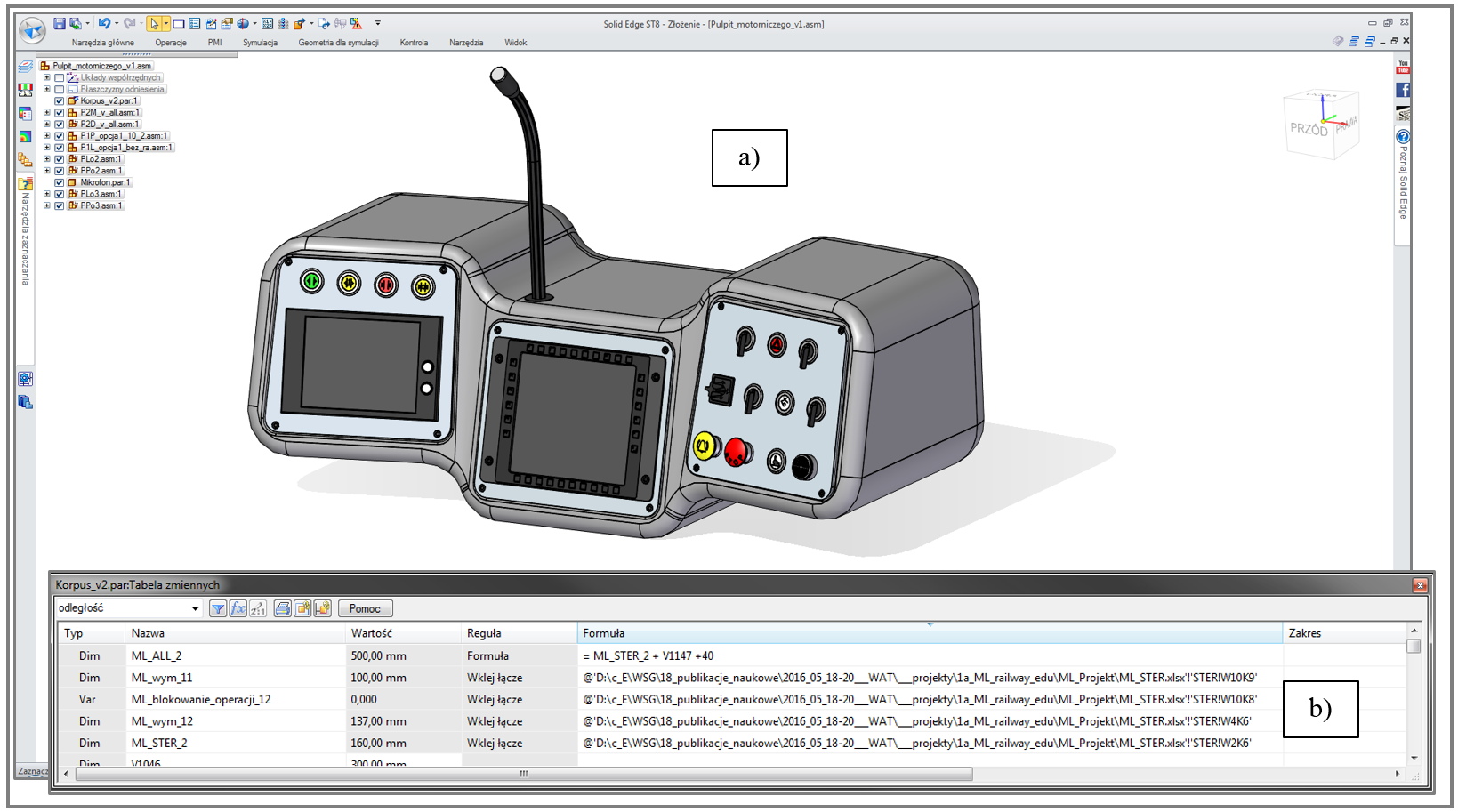
(warto porównać z danymi wejściowymi w pliku .XLSX przedstawionymi na rys. 3.1.3).
Wybrane odmienne warianty modelu opisywanego pulpitu, o geometrii uzależnionej od łącznego wyboru dokonanego w ‘sterującym piku’ .XLSX – dodatkowo różnej od przedstawionej na rys. 3.1.4. – zademonstrowano na rys. 3.1.5, 3.1.6, 3.1.7 oraz 3.1.8. Wyróżniono tam najlepiej widoczne różnice geometryczne.
Uwagę zwraca m.in. wartość wymiaru X modelu pulpitu, zależna od wybranego trybu jazdy tramwaju, co przedstawiono na rys. 3.1.9.
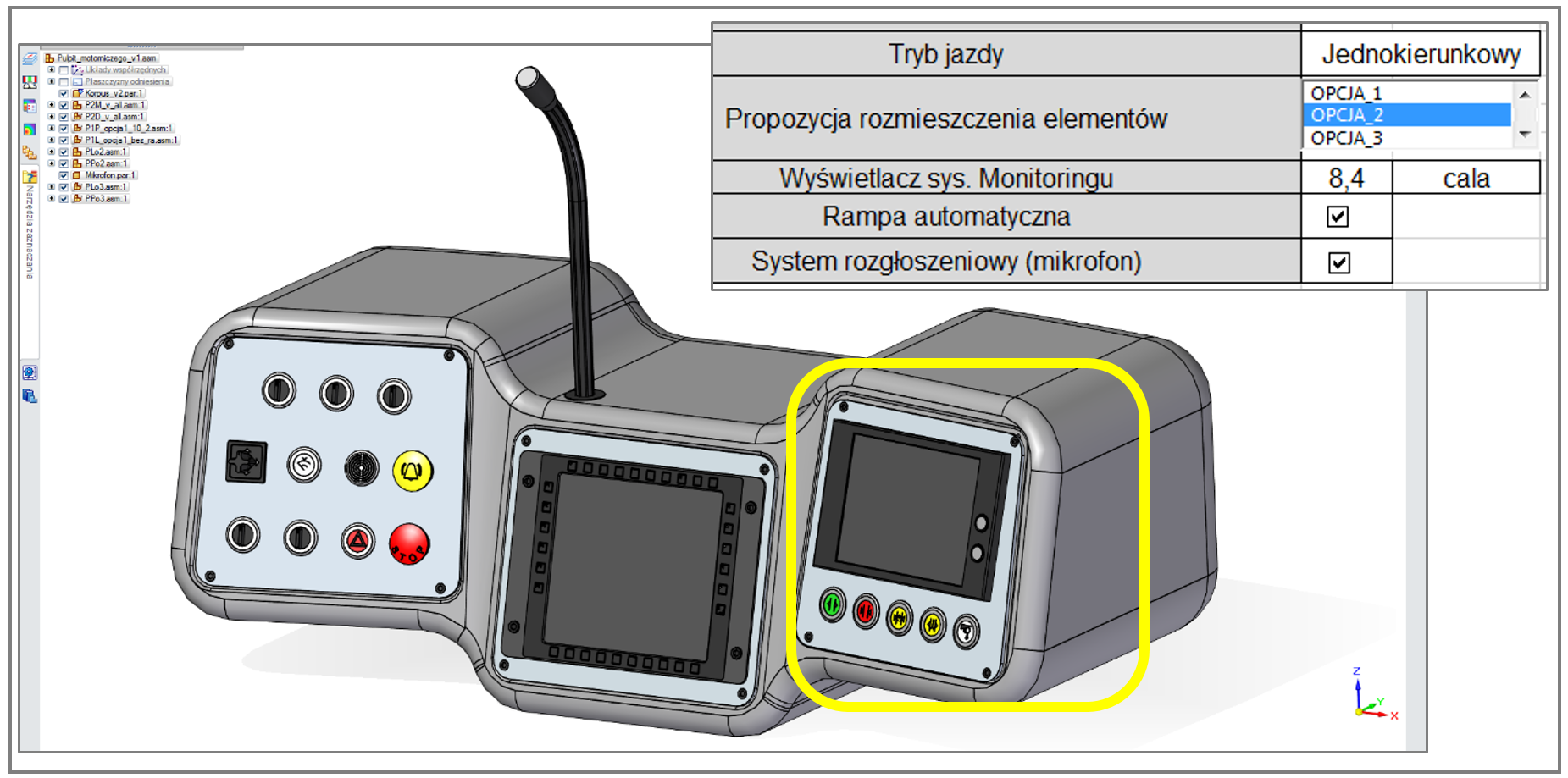
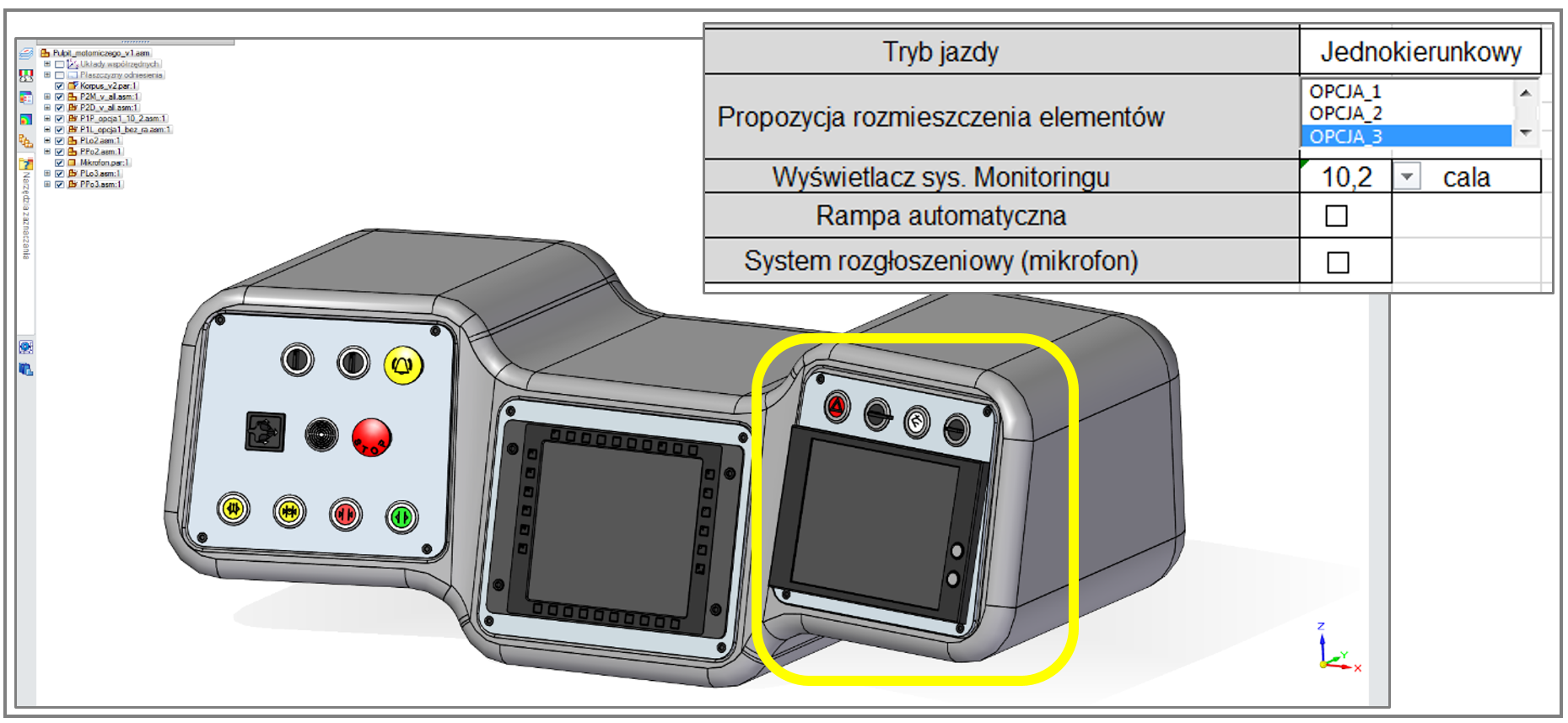
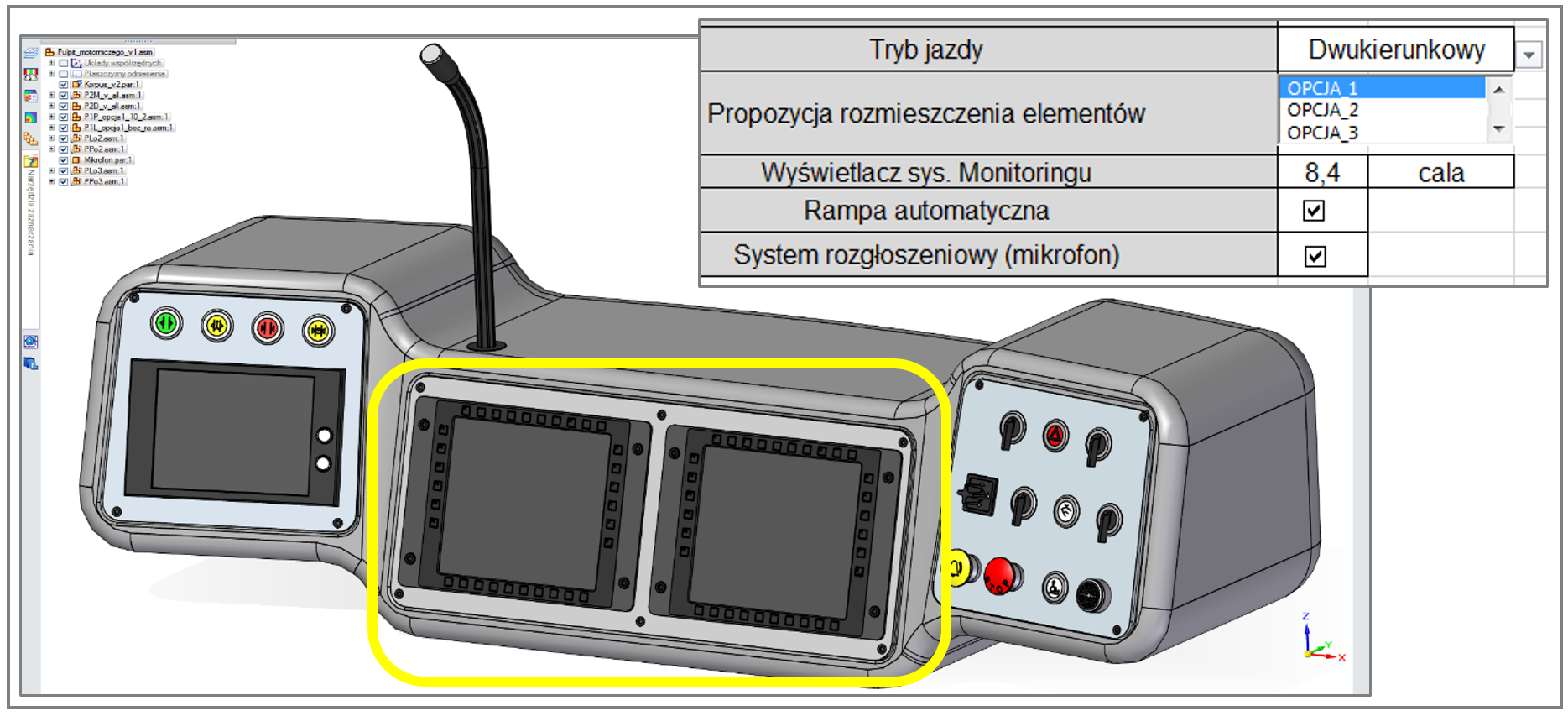
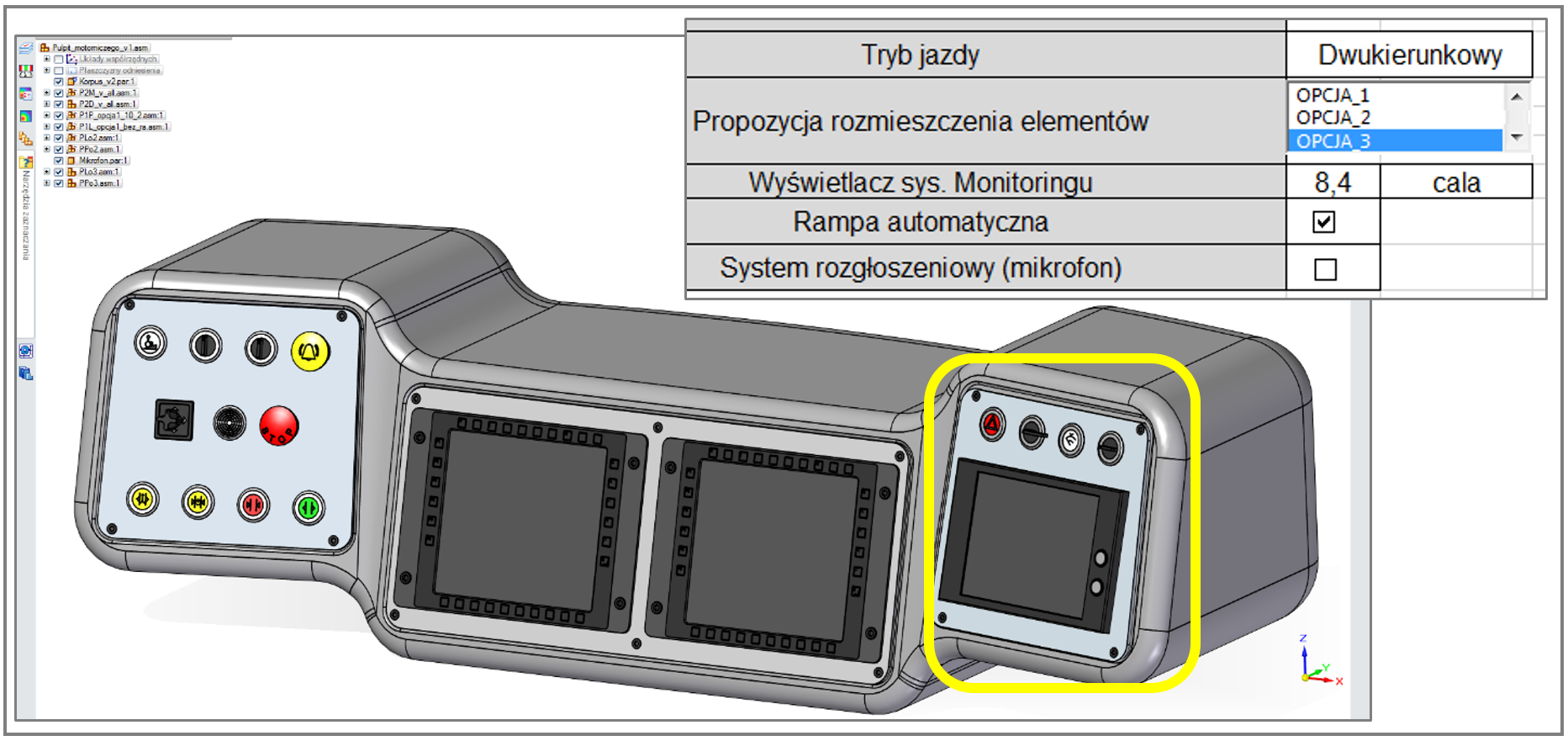
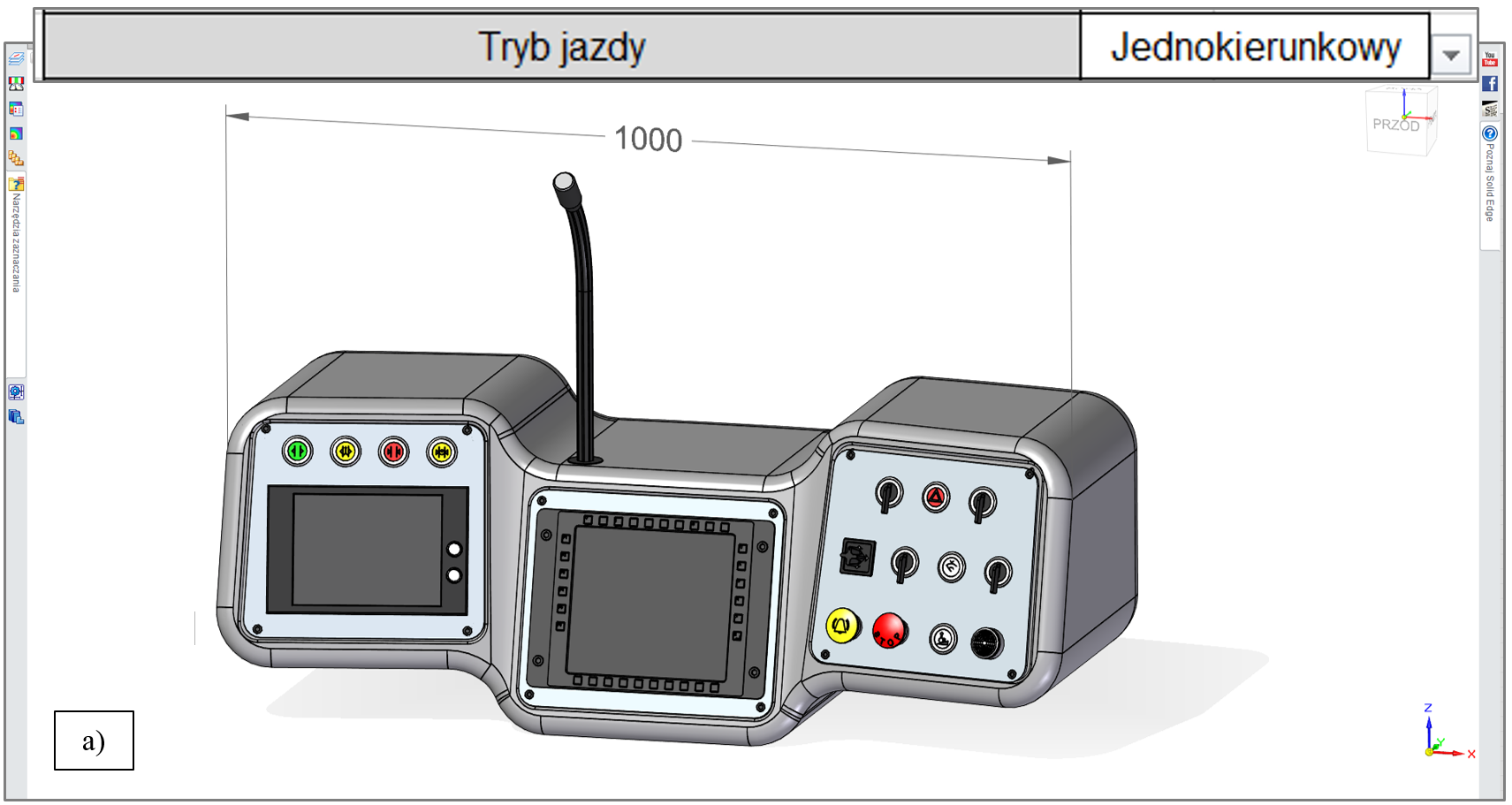
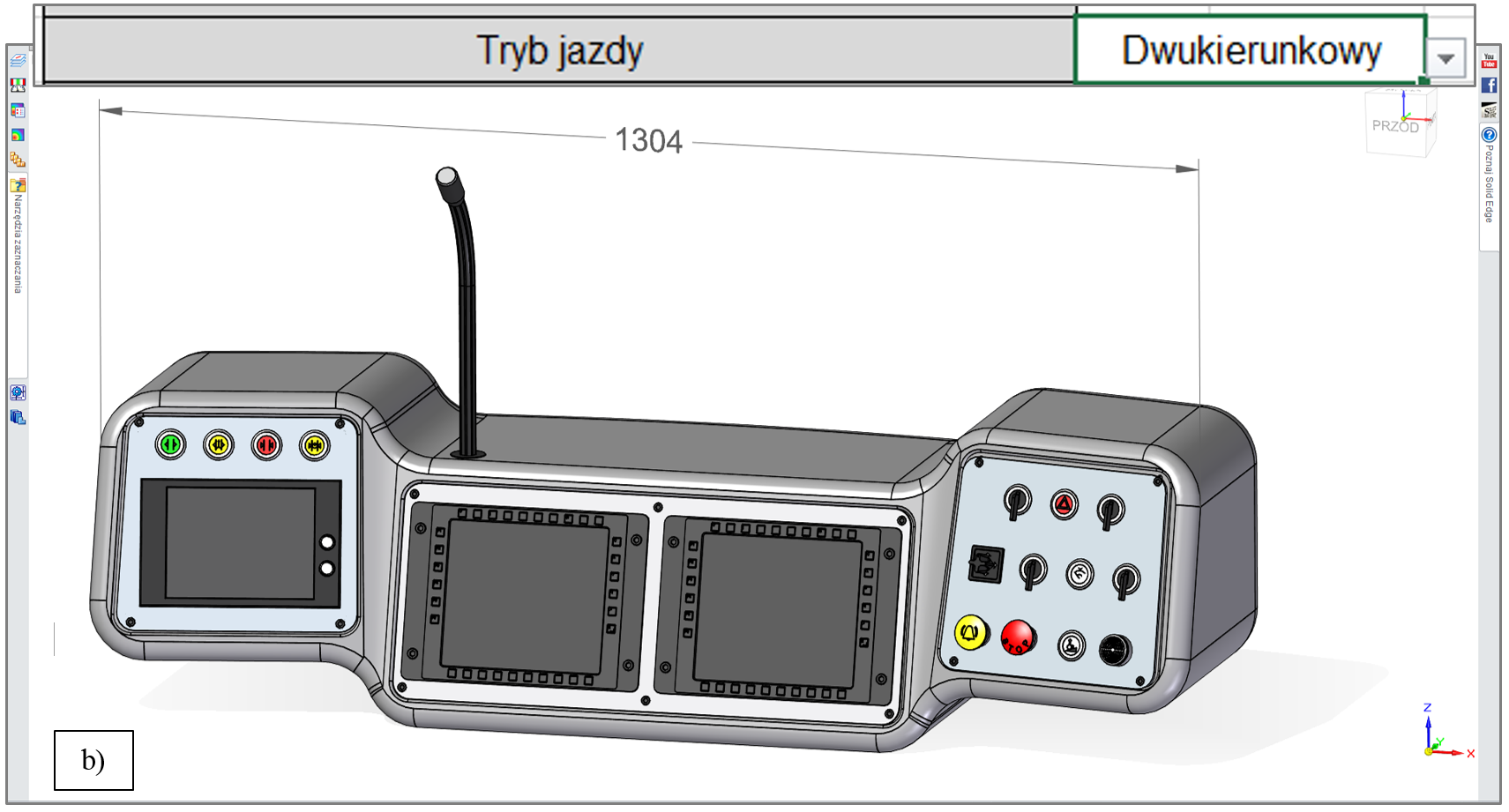
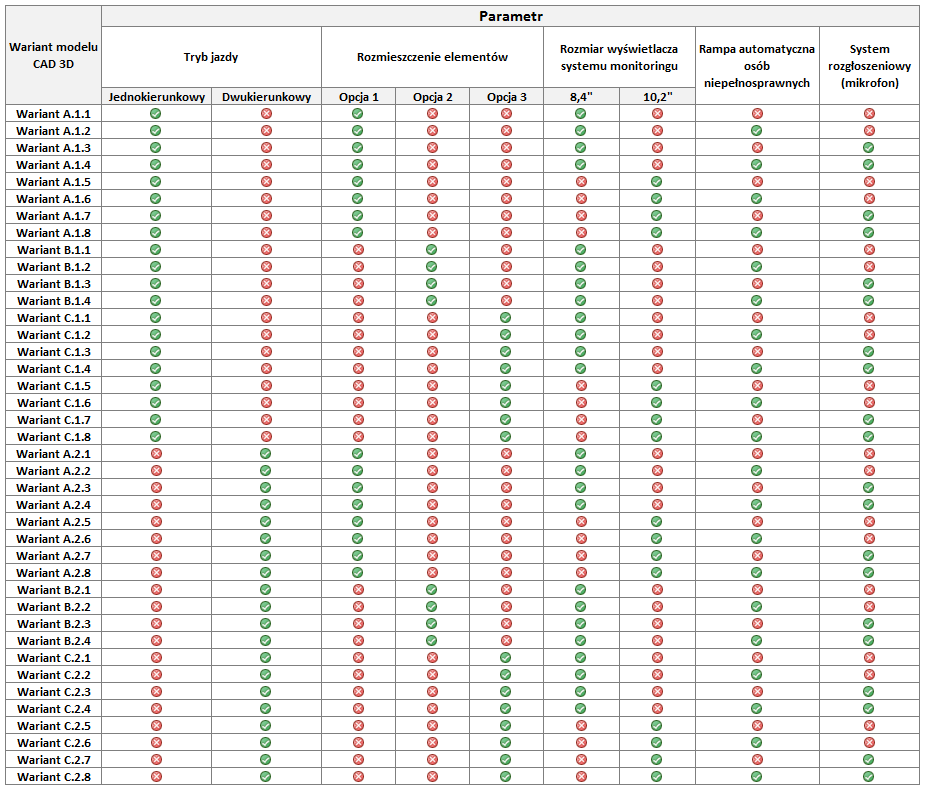
Na rys. 3.1.3. – 3.1.9 przedstawiono kilka spośród autentycznie znaczącej liczby wersji modelu CAD, możliwych do utworzenia na podstawie łącznego wyboru dokonanego w arkuszu .XLSX. Kompletne ‘spektrum’ wariantów modelu pulpitu tramwaju przedstawiono w tabeli na rys. 3.1.10.
Warto pamiętać, iż wraz z utworzeniem odpowiedniego modelu 3D, właściwej aktualizacji ulega także m.in. odpowiednia dokumentacja 2D (rys. 3.1.11, o treści adekwatnej względem rys. 3.1.4.)
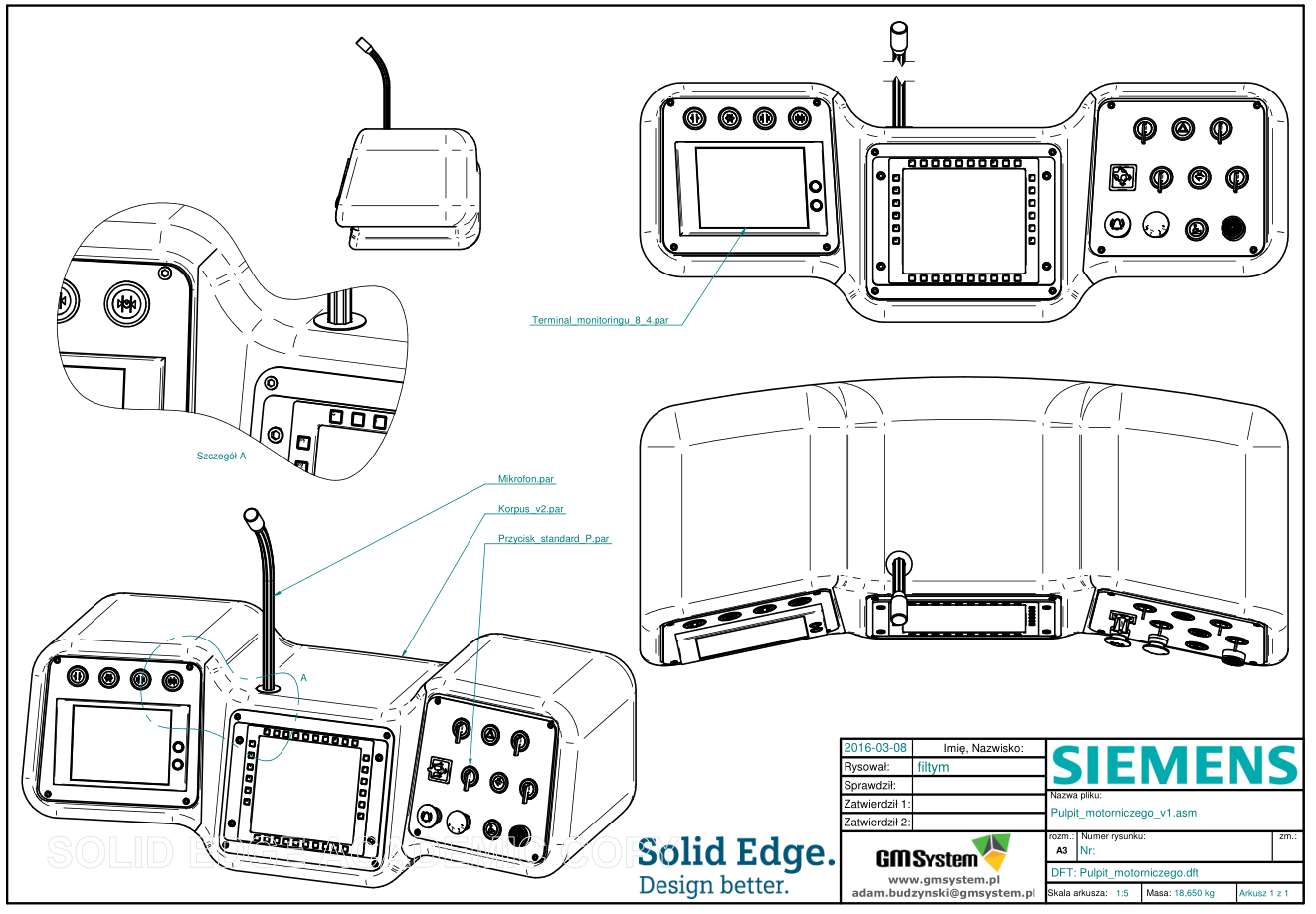
3.2 Przykład z branży motoryzacyjnej
Jednym z wyznaczników zaawansowania technicznego rozwiązań do modelowania parametrycznego CAD jest możliwie rozbudowana liczność i złożoność zmian, które można wprowadzić w modelu, z jednoczesnym zwróceniem uwagi na maksymalne uproszczenie obsługi zintegrowanych środowisk (3D/2D oraz baza danych w MS EXCEL).
Niniejszym przedstawione zostanie rozwiązanie, pełniące rolę konfiguratora geometrii modelu 3D transportowej przyczepy samochodowej, które to rozwiązanie wyróżnia się pozytywnie pod względem obydwu ww. zalet.
Proces parametrycznego i wielo-wariantowania modelowania można podzielić tutaj na następujące etapy:
Etap 1. Uruchomienie środowisk MS EXCEL + SIEMENS SOLID EDGE, ekran powitalny, wygenerowanie modelu dla domyślnych wartości rozpatrywanych parametrów (rys. 3.2.1),
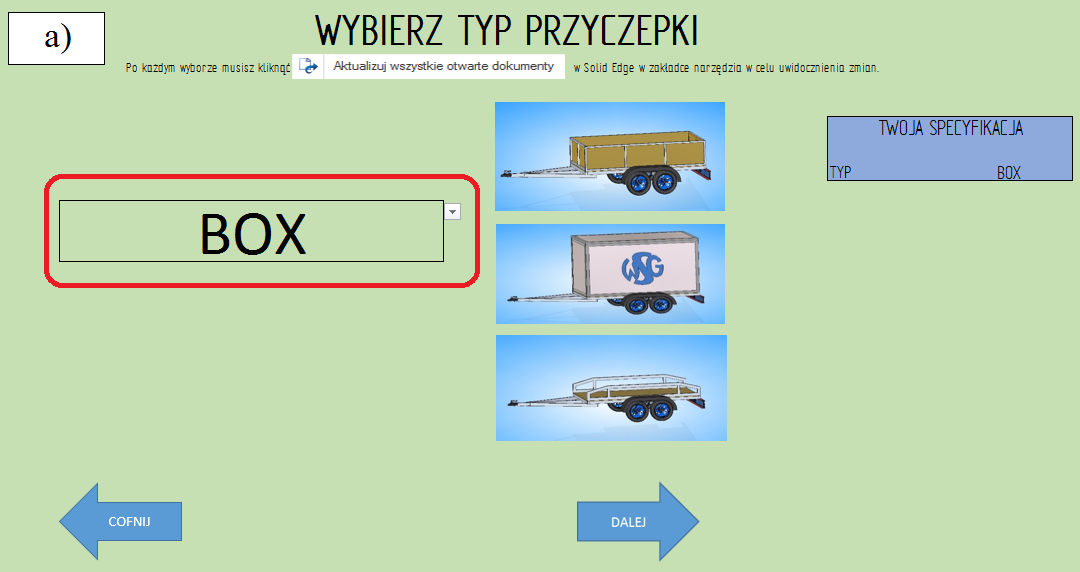
Etap 2. Wybór rodzaju przyczepy do późniejszego uszczegółowienia wymiarów:
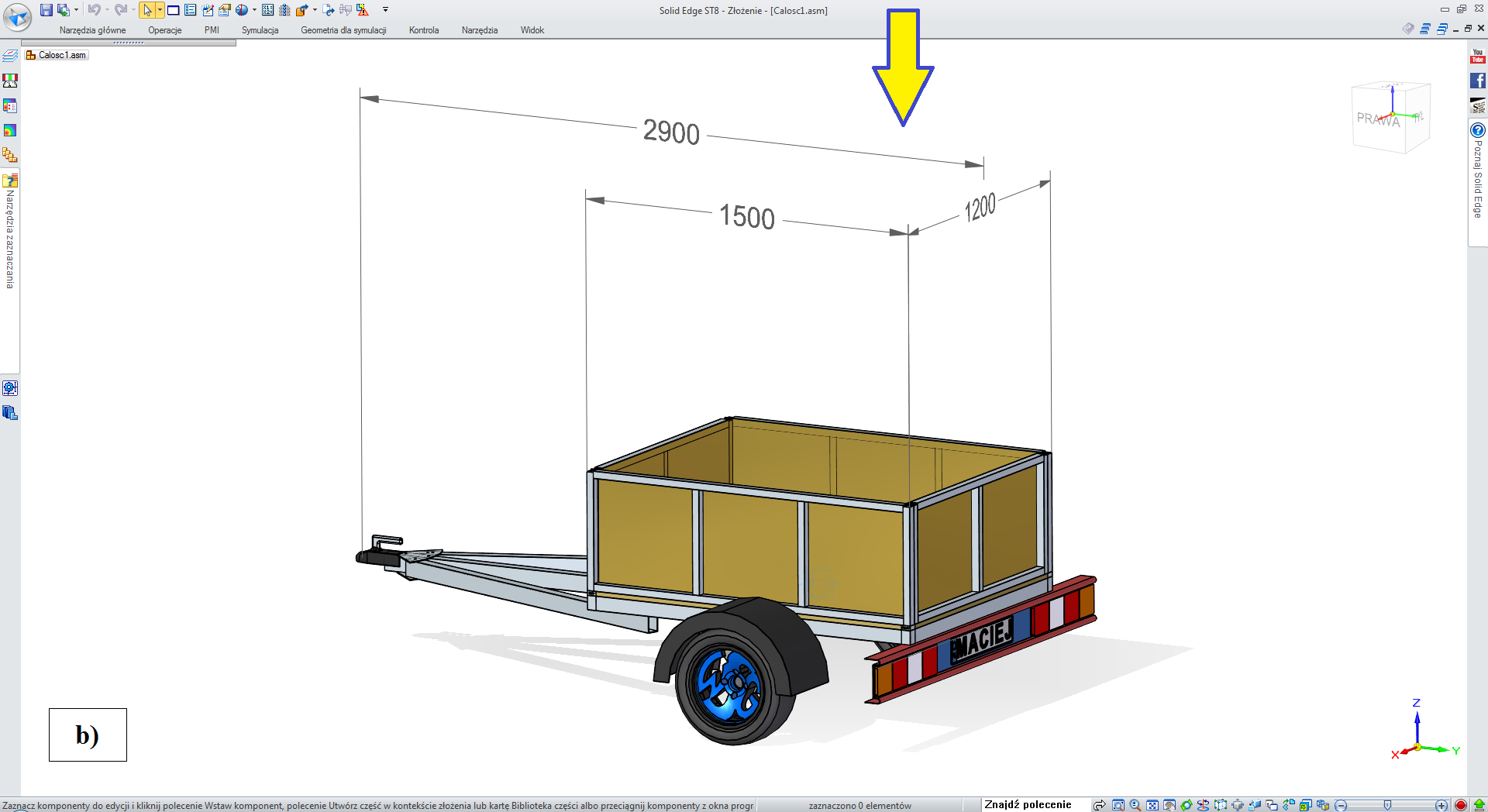
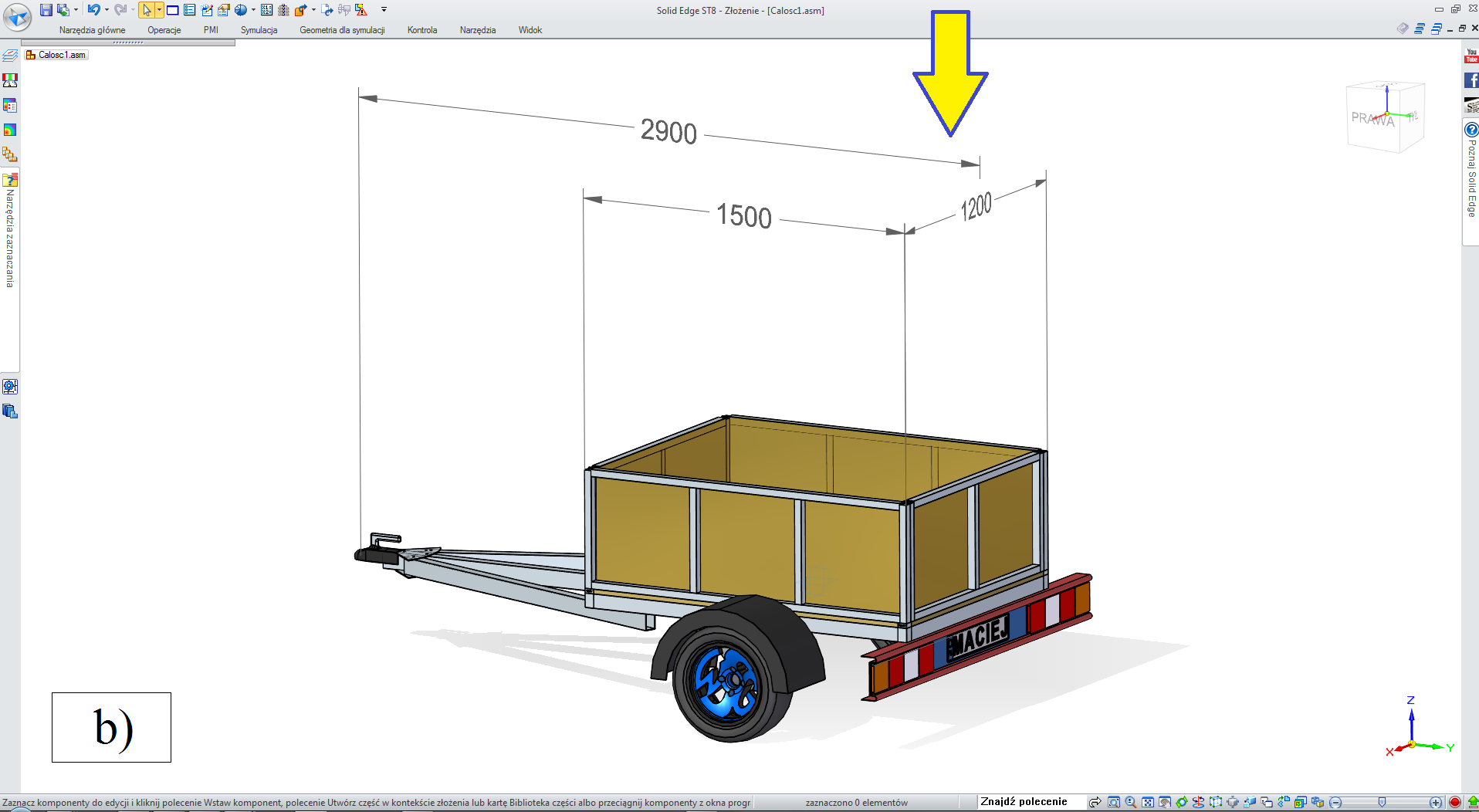
• „towarowa” (rys. 3.2.2-1),
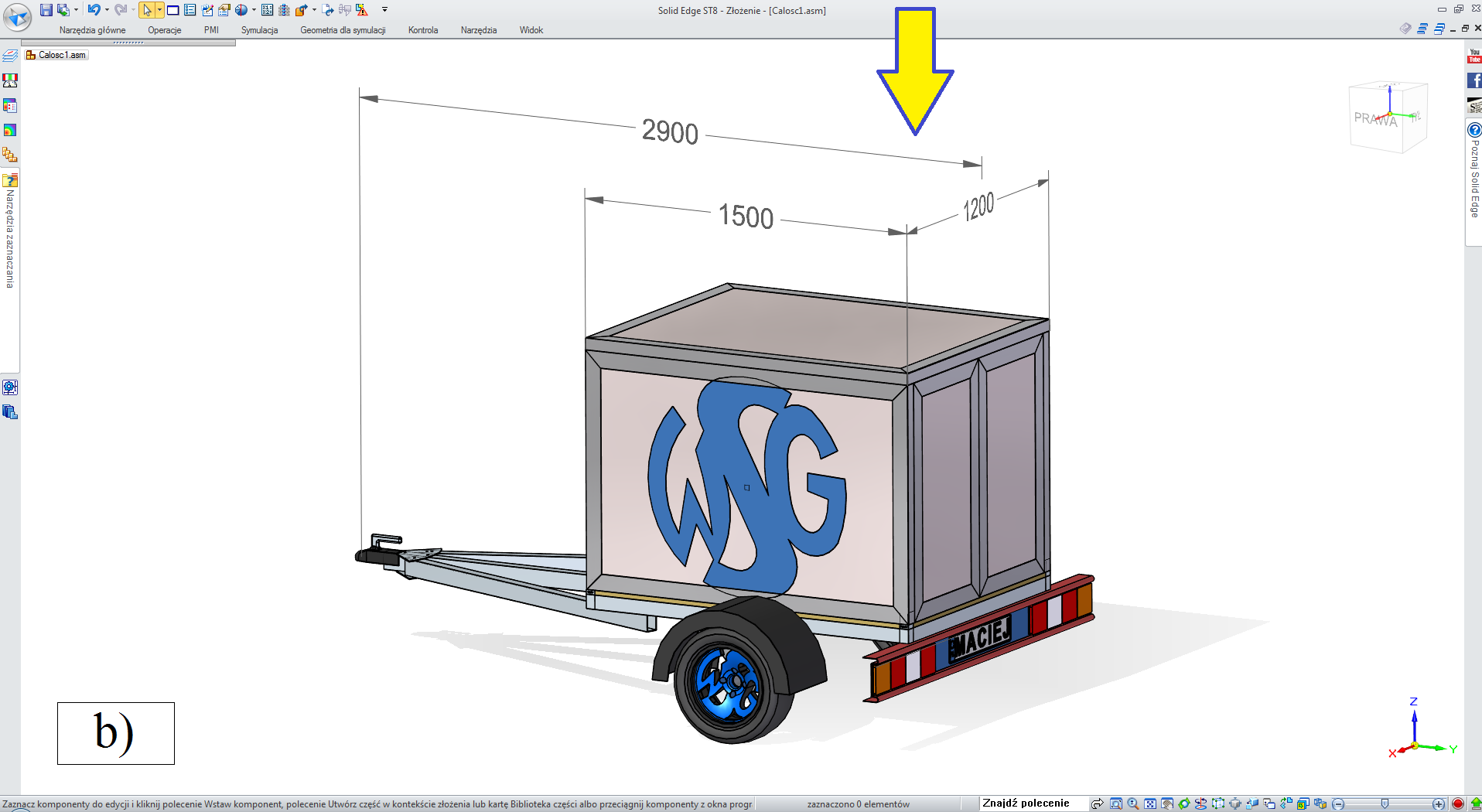
• „box” (rys. 3.2.2-2),
• „laweta” (rys. 3.2.2-3),
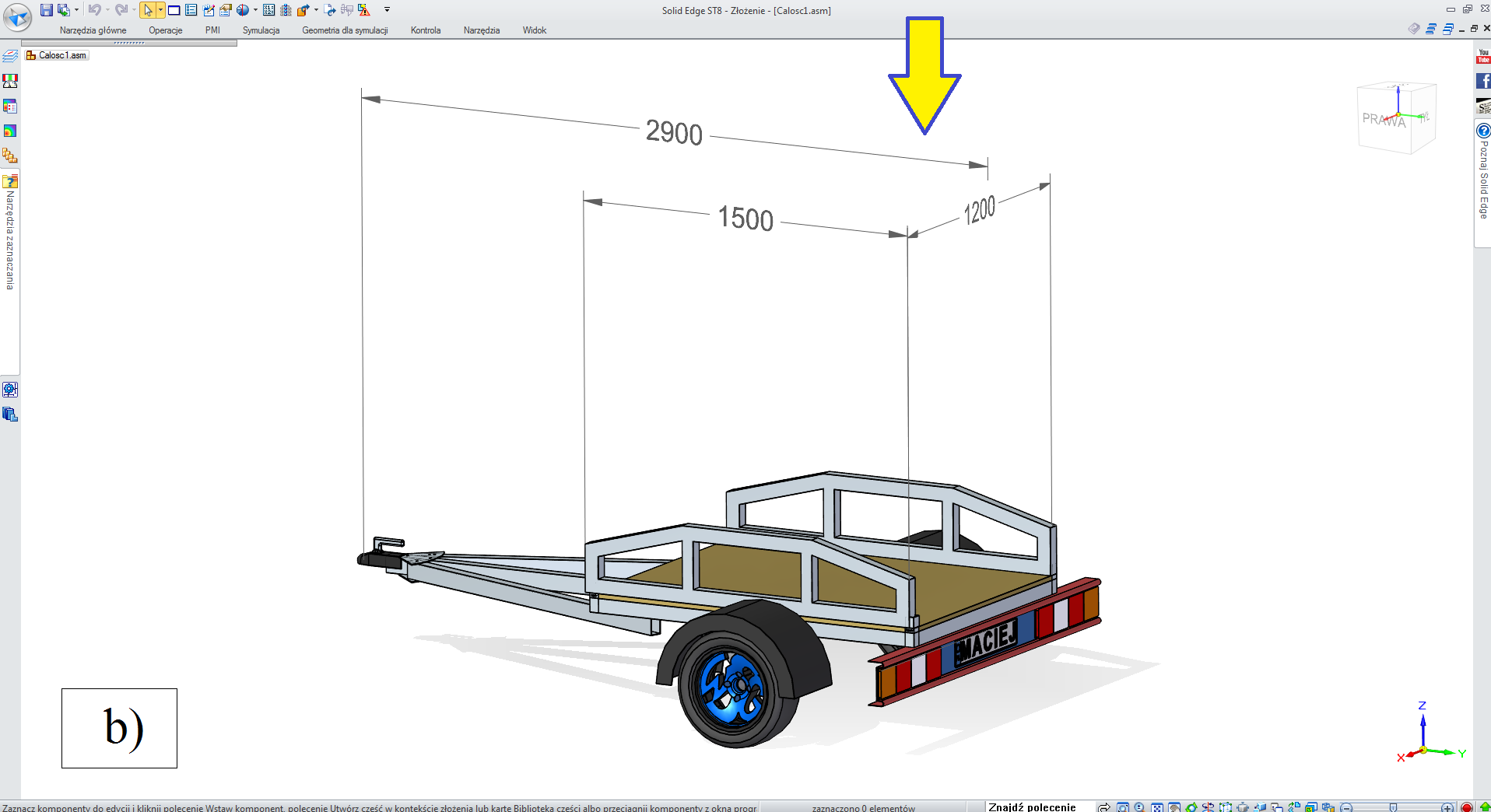
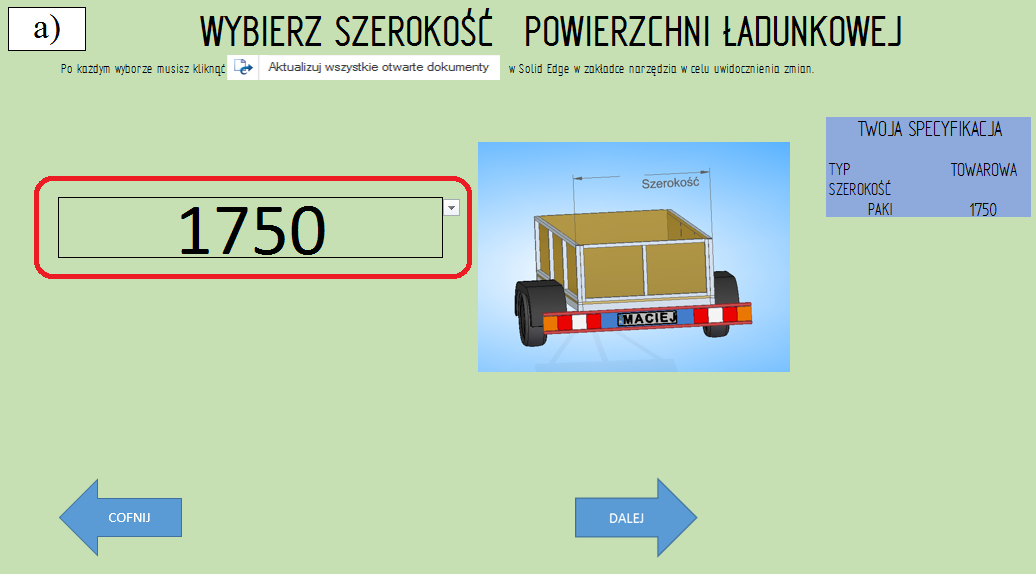
Etap 3. Wybór (ew. pozostawienie) wymiaru szerokości, na podstawie zbioru wartości predefiniowanych (rys. 3.2.3),
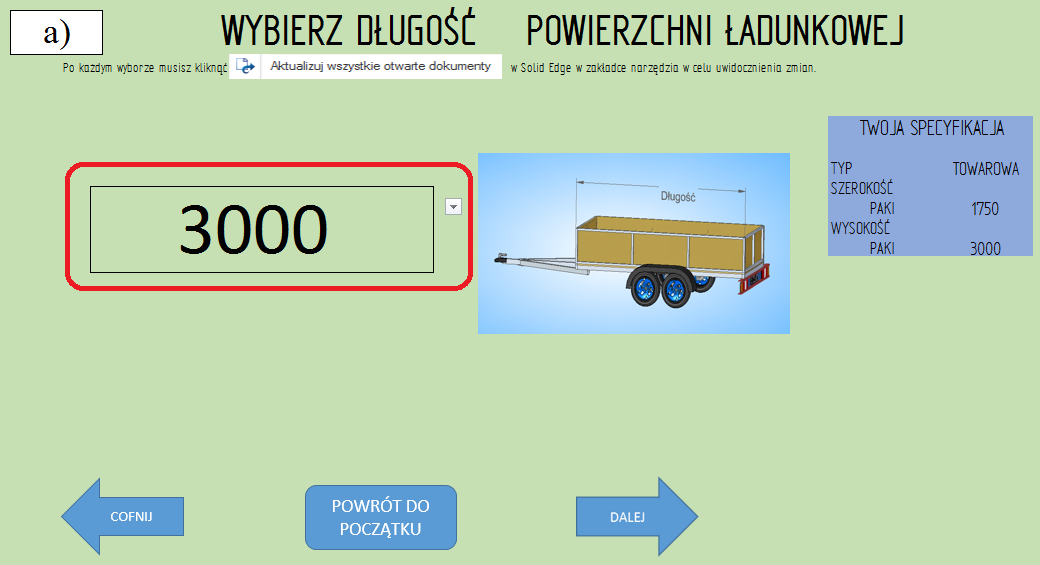
Etap 4. Wybór (ew. pozostawienie) wymiaru długości, na podstawie zbioru wartości predefiniowanych (rys. 3.2.4).
Uwagę zwraca fakt, iż w zależności od wartości długości, system samoczynnie dobiera właściwą liczbę osi.
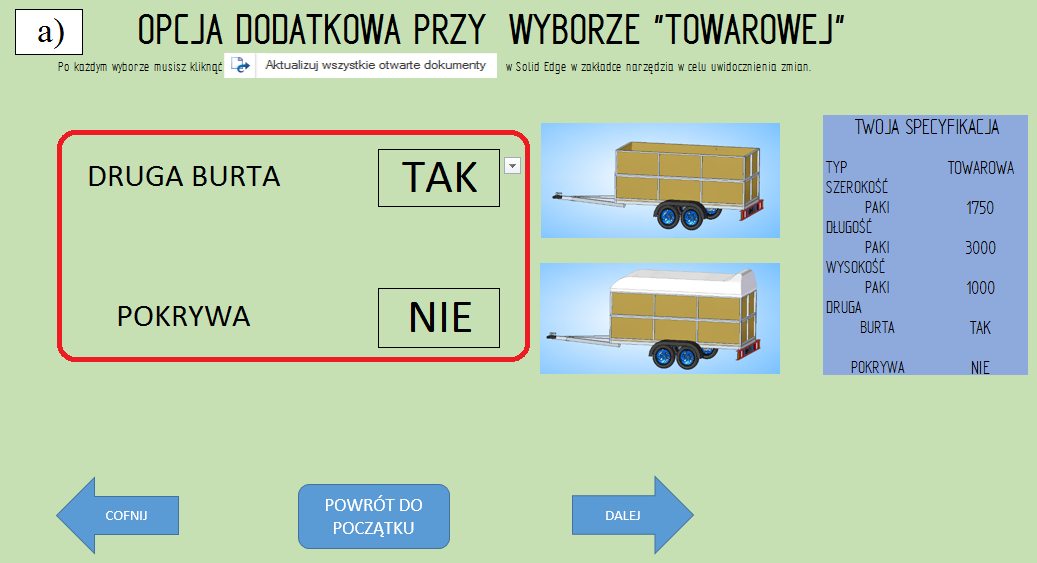
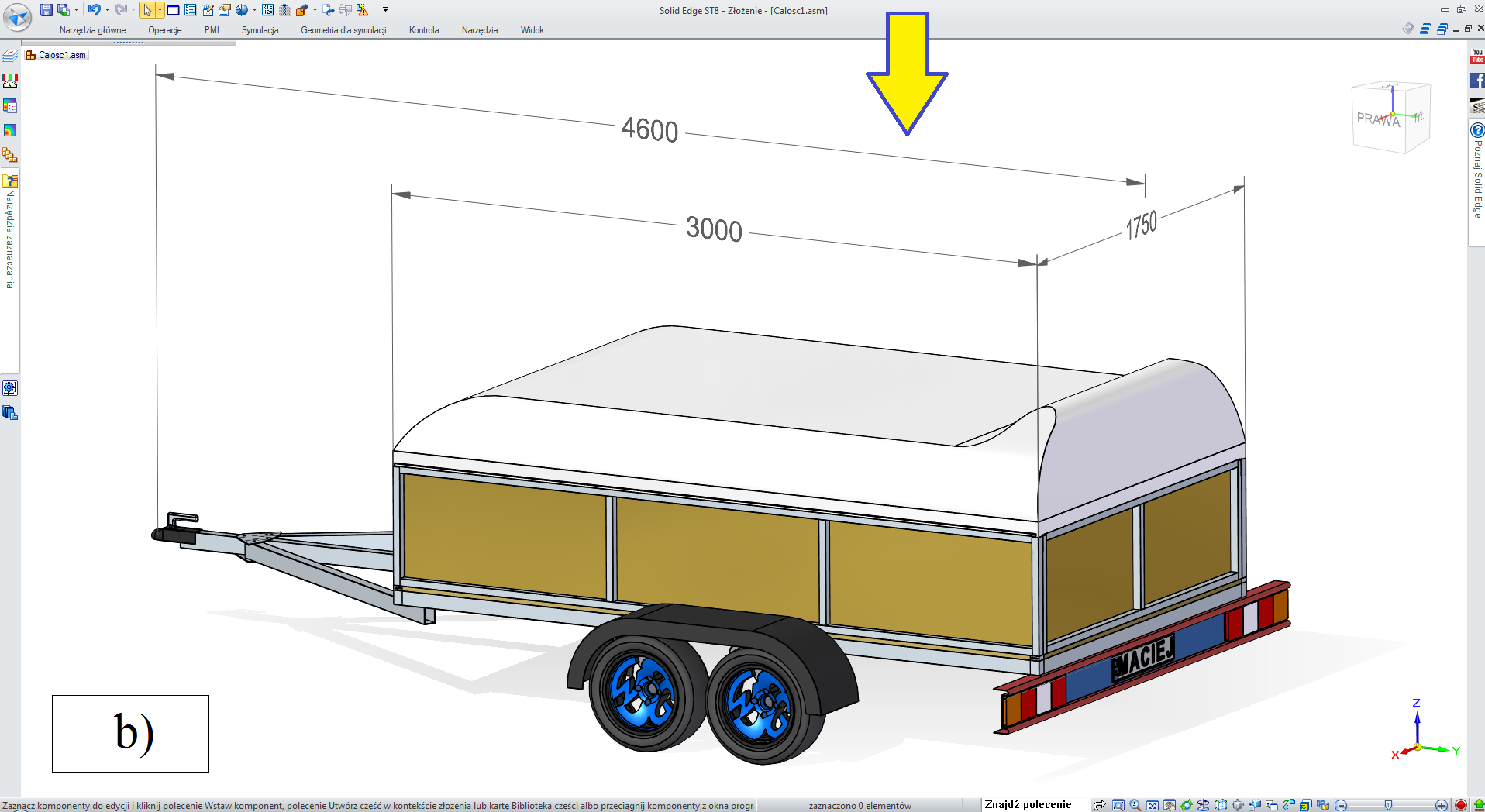
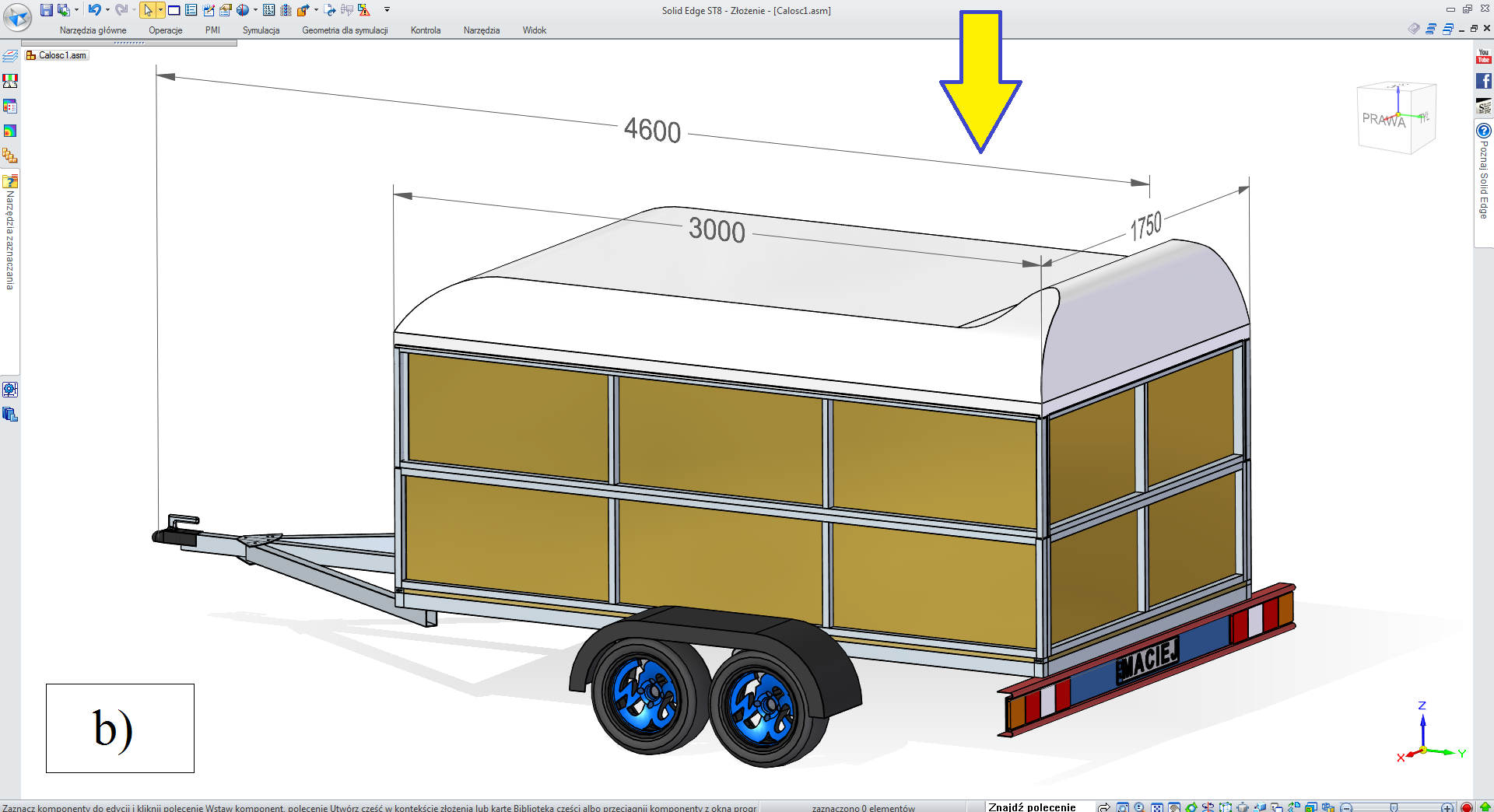
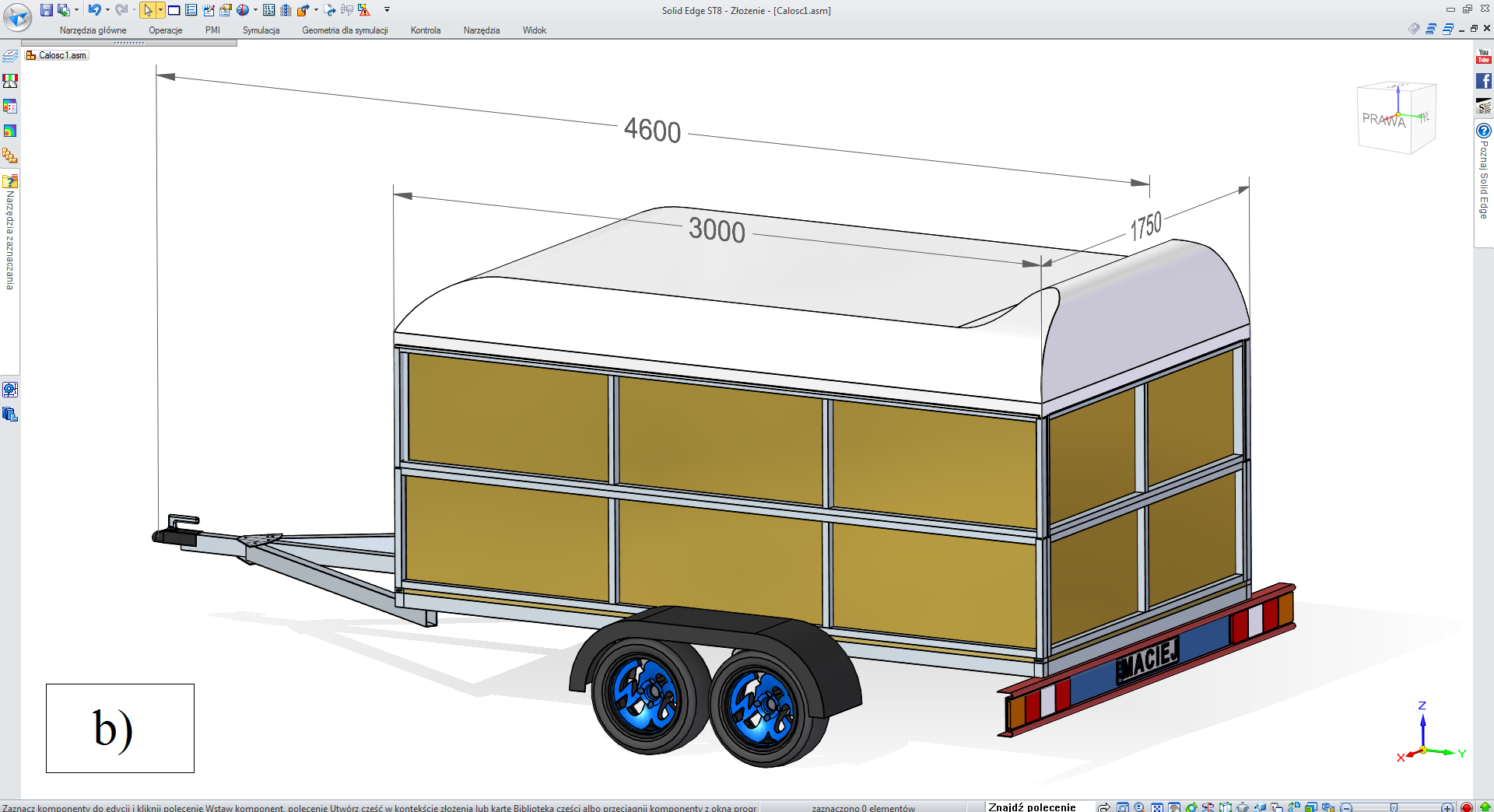
Etap 5. Opcje dodatkowe dla przyczepy „towarowej’,
• „druga burta” NIE, „pokrywa” NIE (jak na rys. 3.2.4),
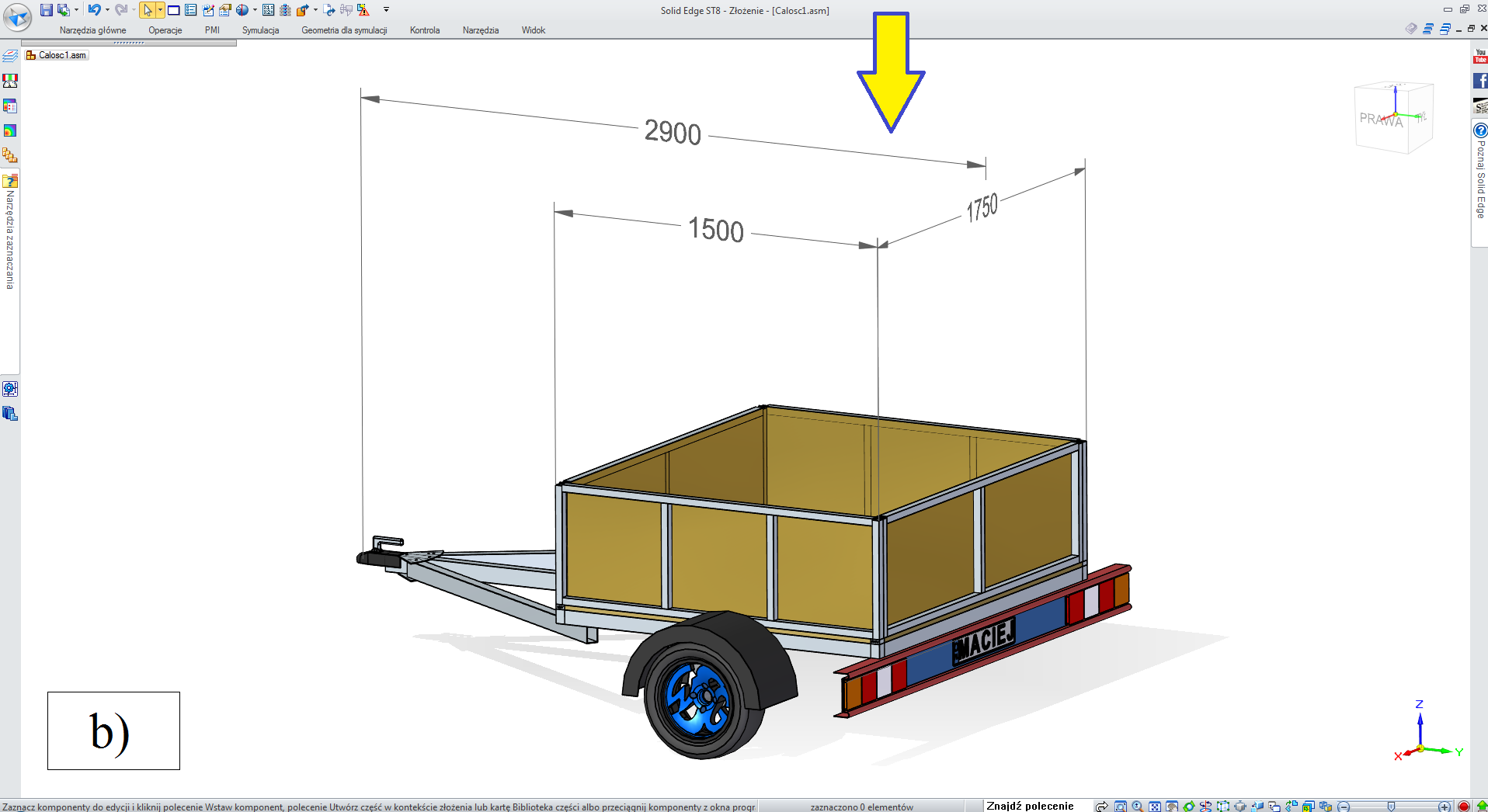
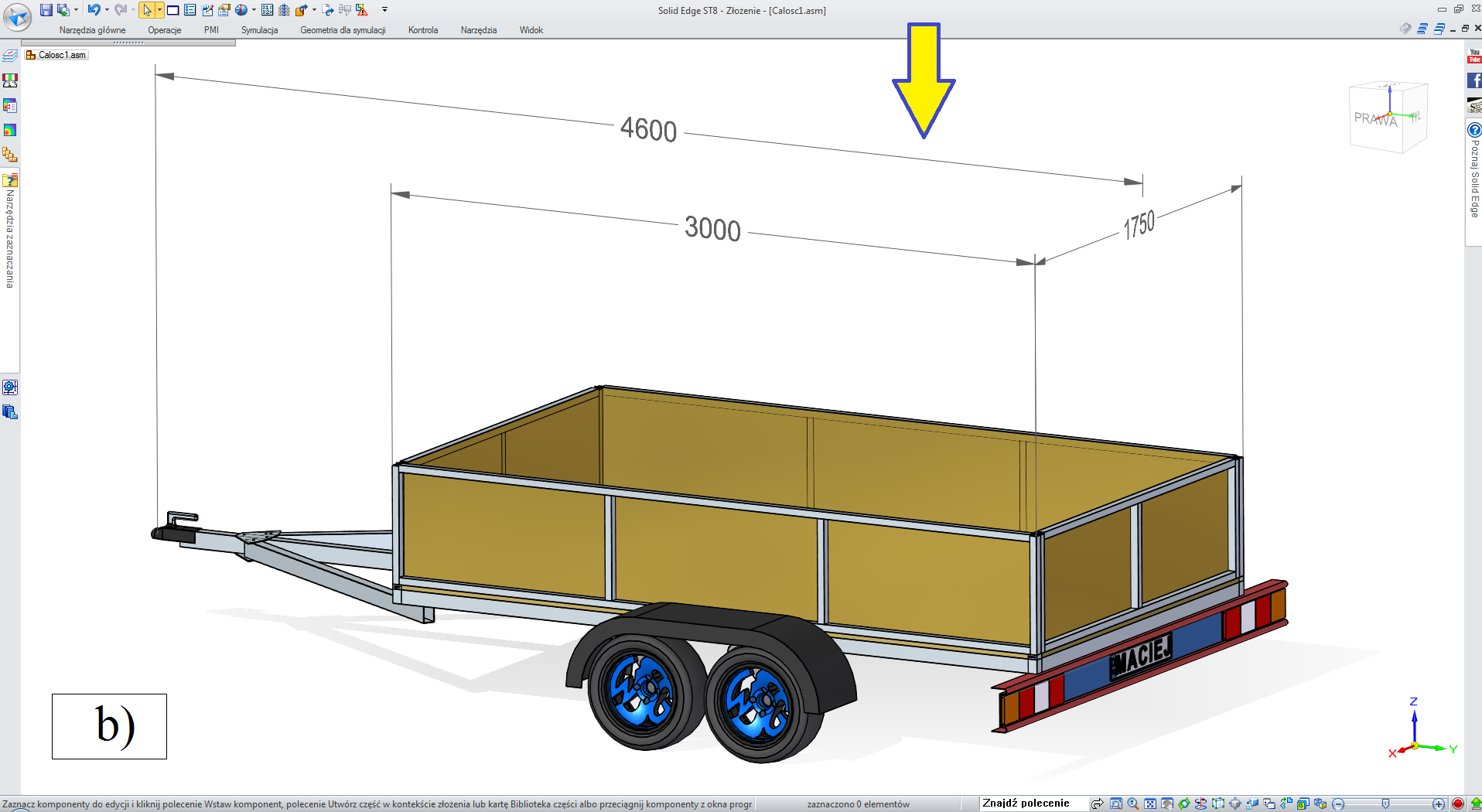
• „druga burta” TAK, „pokrywa” NIE (rys. 3.2.5-1),
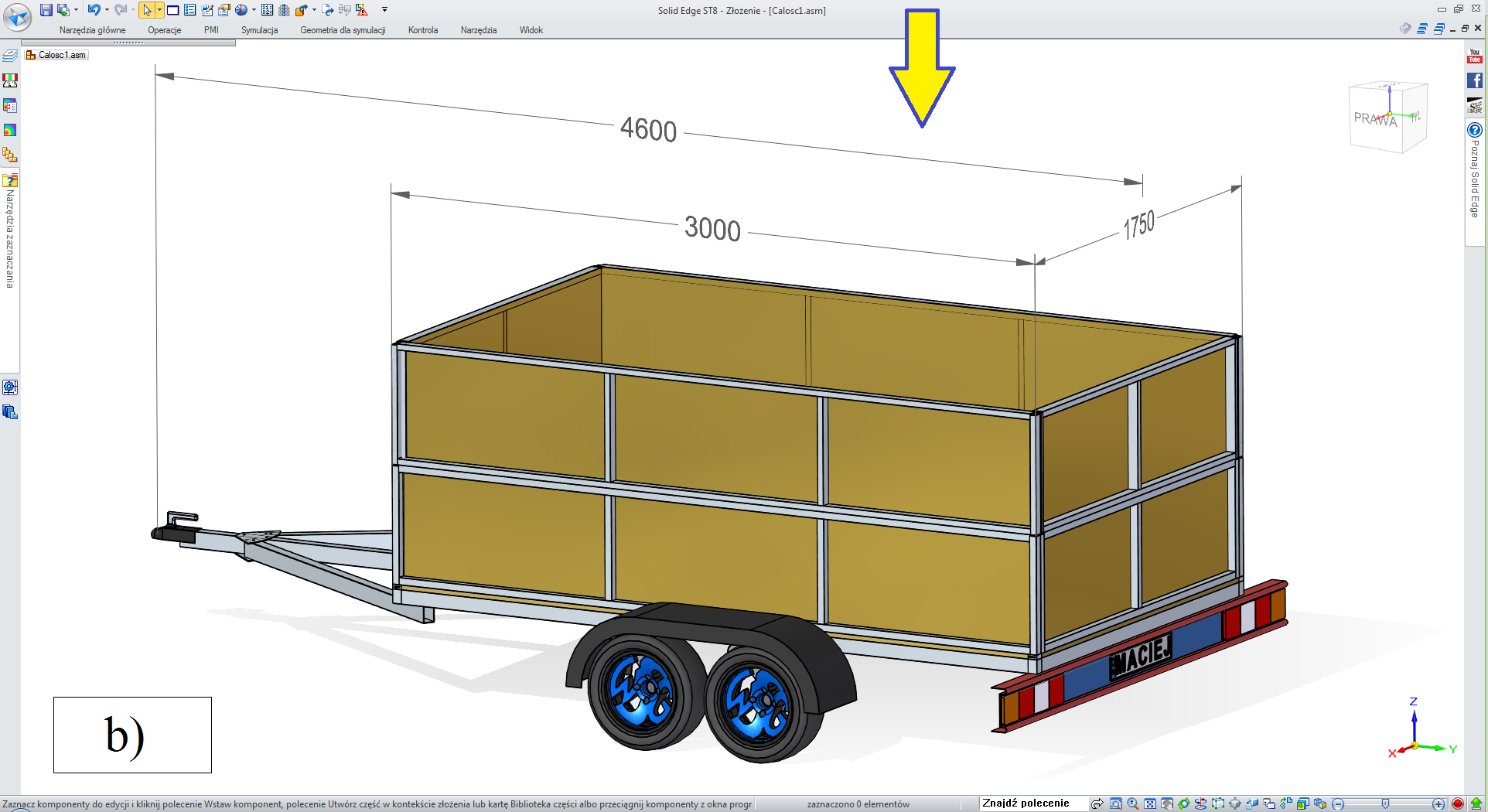
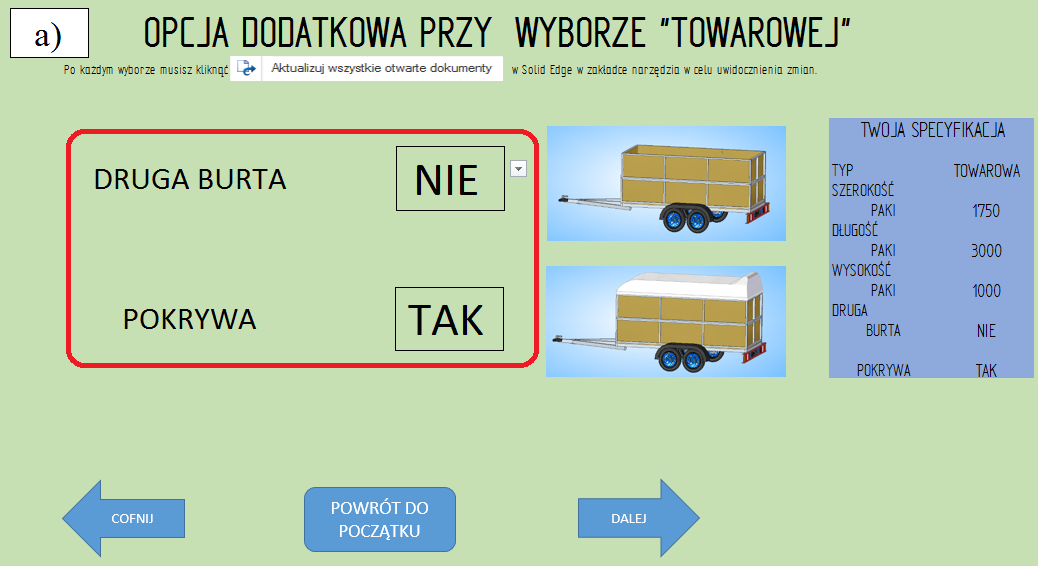
• „druga burta” NIE, „pokrywa” TAK (rys. 3.2.5-2),
• „druga burta” TAK, „pokrywa” TAK (rys. 3.2.5-3),
Etap 6. Zakończenie pracy, wyświetlenie zestawienia zbiorczego wprowadzonych parametrów (rys. 3.2.6).


a) MS EXCEL
a) MS EXCEL, b) SIEMENS Solid Edge.
a) MS EXCEL

a) MS EXCEL
a) MS EXCEL
a) MS EXCEL
a) MS EXCEL

a) MS EXCEL
4. Spersonalizowane formaty w arkuszach Excel
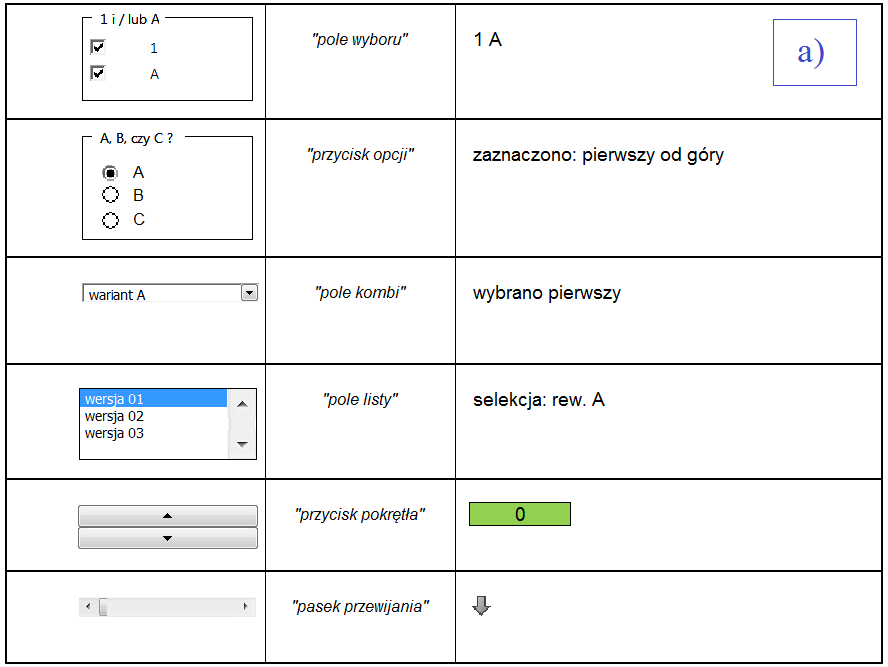
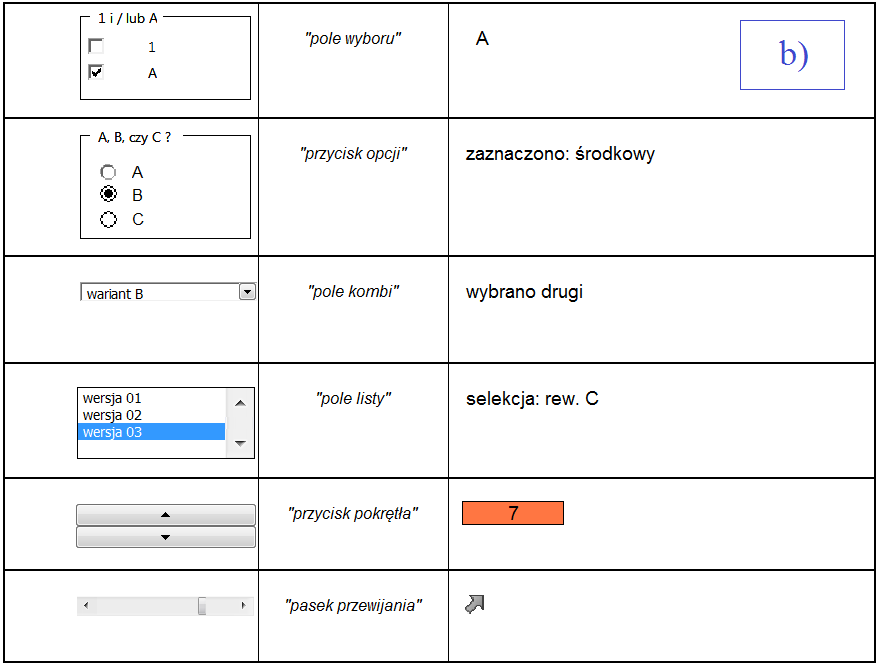
W celu możliwie wygodnego oraz intuicyjnego zarządzania danymi w arkuszach danych, obydwa opisane tu pliki .XLSX wyposażono w spersonalizowane formanty (rys. 4.1), m.in. takich rodzajów, jak:
– pole wyboru,
– przycisk opcji,
– pole kombi,
– pole listy,
– przycisk pokrętła,
– pasek przewijania.
5. Optymalizacja CAD
Po właściwym ‘sparametryzowaniu’ modelu CAD, możliwe jest przeprowadzenie jego optymalizacji,
tj. np. znalezienie takiej jego postaci geometrycznej, dla której wartości wskazanych wielkości (np. fizycznych typu masa, lokalizacja środka masy, tzw. „strzałka ugięcia”, itd.) uzyskają żądaną wartość (optymalną, tj. idealną).
W opisywanym przypadku, proces optymalizacji jest zautomatyzowany i realizowany metodą kolejnych iteracji.
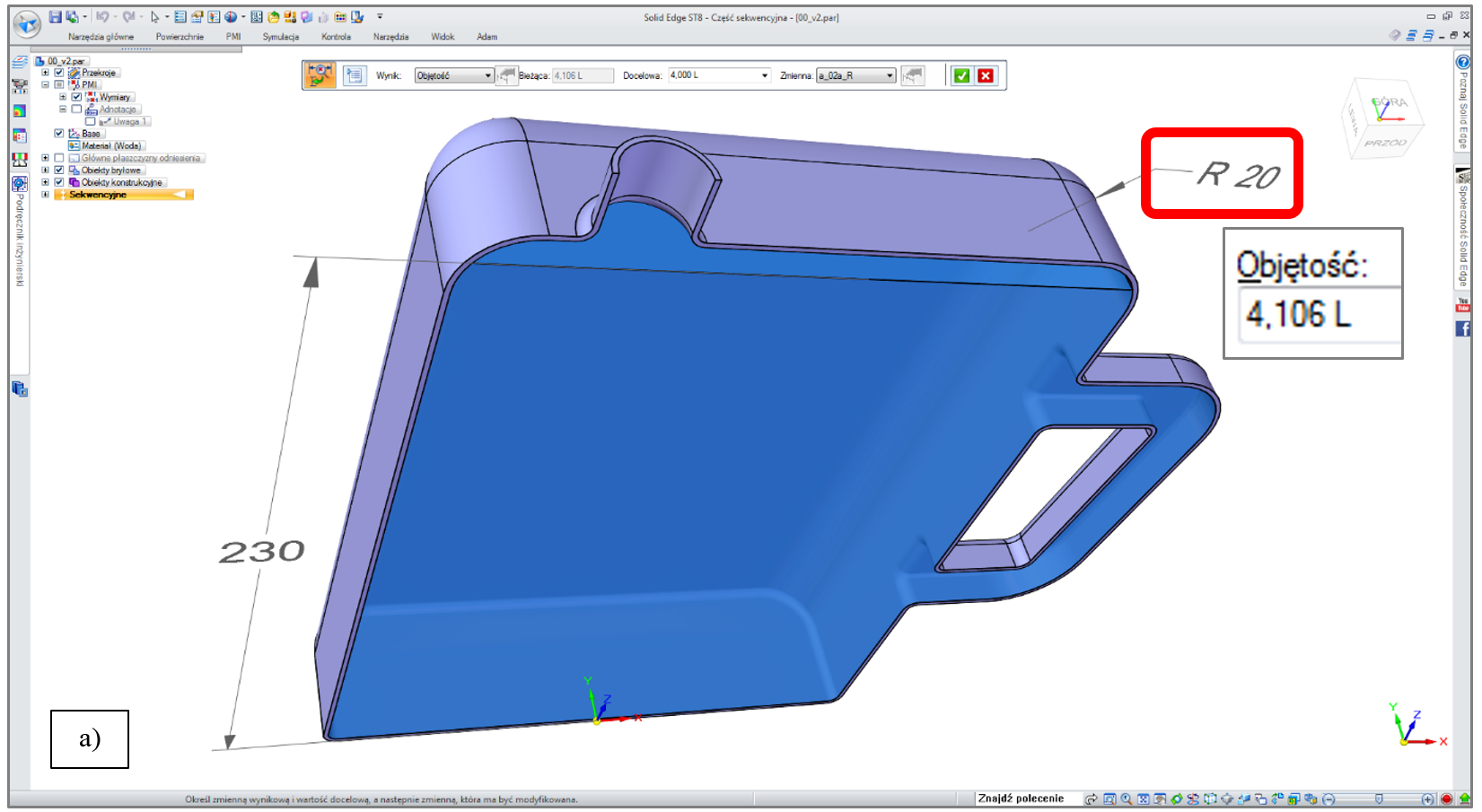
Na rys. 5.1.a przedstawiono model butelki polimerowej (w celowym przekroju 3D), której objętość wnętrza
do założonego „poziomu lustra cieczy” jest większa, niż docelowe 4 L, co oznaczać może stratę ponoszoną przez podmiot sprzedający, jeżeli przedmiotem transakcji jest ciecz w ilości dokładnie 4 L.
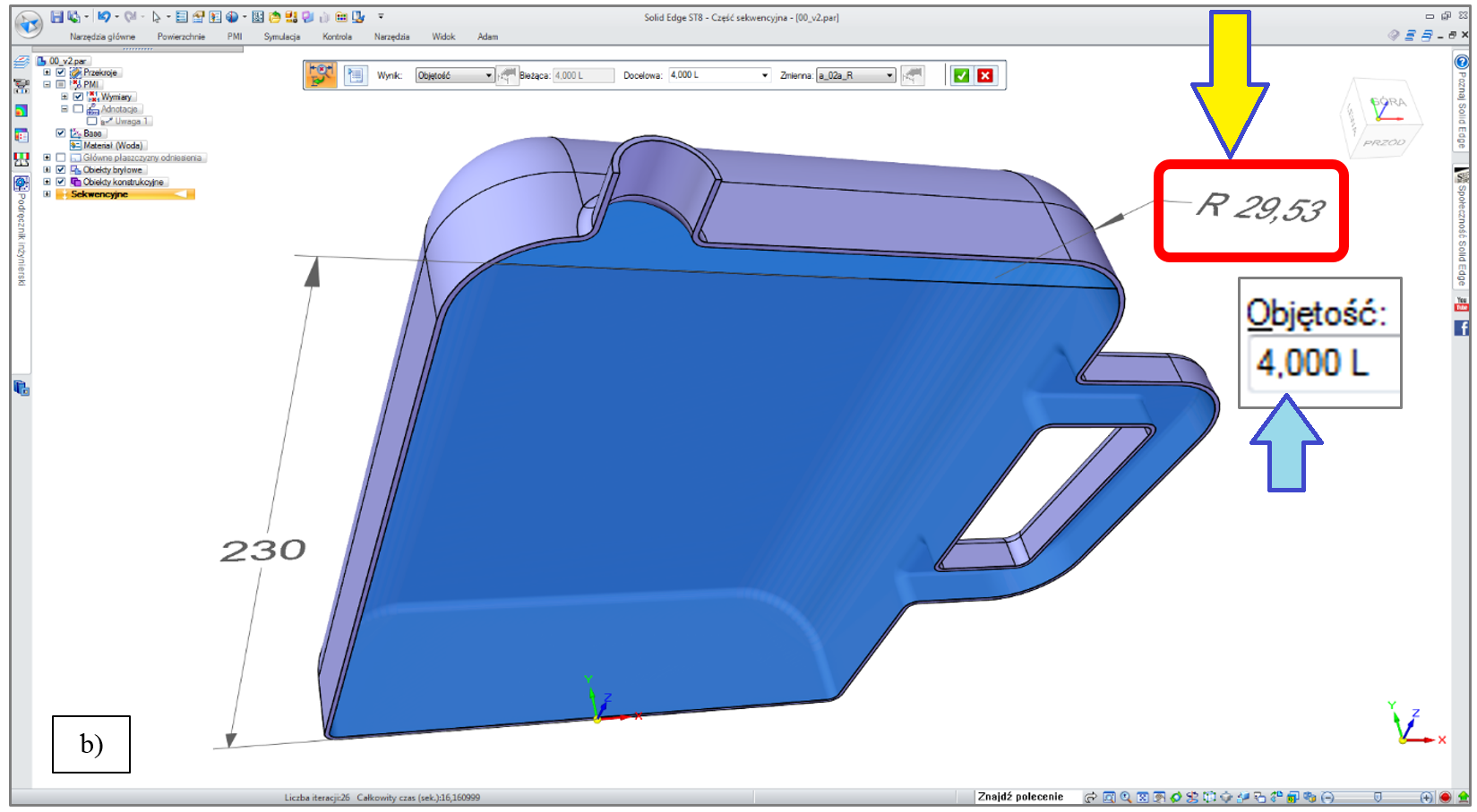
W omawianym przypadku, zadanie polega na znalezieniu takiej wartości promienia zaokrąglenia górnych krawędzi butelki, aby objętość jej wnętrza do ww. „poziomu lustra cieczy” wynosiła dokładnie 4 L.
Model 3D butelki po samoczynnym rozwiązaniu tego zadania przez system CAD przedstawiono na rys. 5.1. b.
6. Wnioski
W wyniku zaistnienia wielo-wariantowość konstrukcji CAD, pojawia się możliwość wygenerowania modeli wielu wersji produktu w stosunkowo krótkim czasie oraz przy relatywnie niewielkim wykorzystaniu zasobów ludzkich i sprzętowych.
Zwraca się uwagę, iż wraz ze zmianą modeli 3D, aktualizacji ulec mogą także:
– listy części (komponentów składowych wyrobu), tzw. BOM (ang. Bill Of Material),
– zestawienia właściwości fizycznych (np. mas, środków mas, objętości, itd.), zarówno dla całości – – złożenia,
jak też dla jego komponentów składowych,
– właściwa dokumentacja 2D (wykonawcza, złożeniowa, obróbkowa, itd.).
W przypadku tradycyjnych metod modelowania, wprowadzenie względnie niewielkich zmian w geometrii może być zadaniem długotrwałym (tj. kosztownym), zwiększając dodatkowo prawdopodobieństwo popełnienia błędów projektowych.
Przedstawione wykorzystane baz danych (na przykładzie arkuszy Microsoft Excel) znacząco wpływa na wzrost aplikacyjności omawianego rozwiązania konstrukcyjnego we współczesnej branży inżynierskiej, gdzie pojęcia dotyczące zarządzania zmianami projektowymi (ECO, ang. Engineering Change Order) wciąż zyskują na znaczeniu. Zachodzi to w uzasadnionym celu ciągłego zwiększania opłacalności działań przemysłowych (tutaj głównie z racji radykalnego zmniejszania kosztów realizacji projektu, docelowo, za każdym razem, gdy zostanie on zastosowany w swej pierwotnej
lub odpowiednio zmienionej formie).
Finalna postać tak uzyskanego rozwiązania cechuje się powtarzalnością oraz łatwością i elastycznością wykorzystania.
Dzięki temu, obsługa tego wydajnego rozwiązania (pod względem właściwej obsługi bazy danych oraz systemu CAD) nie wymaga od użytkownika wiedzy eksperta. Wręcz przeciwnie. Uważa się, iż już średnia znajomość przedstawionych tu narzędzi IT umożliwia ich właściwe zastosowanie w praktyce inżynierskiej.
Dodatkowo, dzięki możliwości przeprowadzania optymalizacji tak wygenerowanych modeli parametrycznych, ze względu na określone kryterium, np. wartości masy lub lokalizacji jej środka, można założyć, iż finalna postać modelu 3D „przebyła drogę” od wersji ‘dobra’, przez ‘lepsza’, aż do ‘najlepsza’.
Całość pretenduje do zaliczenia do nowego podejścia do projektowania. Rezygnuje się tutaj z tworzenia modelu „od początku dla każdego nowego klienta” na korzyść aż i tylko jednego modelu „gotowego do szybkiej i zautomatyzowanej zmiany do nowej postaci oczekiwanej przez istniejącego, a zwłaszcza kolejnego klienta”.
Autorzy mają świadomość, iż opisane tu tzw. „elastyczne projekty” powstają nieco dłużej, niż gdyby to miało miejsce z wykorzystaniem tradycyjnych metod prowadzenia prac CAD (tj. bez złożonej parametryzacji). Jednakże autorzy uważają, iż docelowo jest to zdecydowanie opłacalne, i ww. początkowy dodatkowy nakład prac należy traktować jako„dobrą inwestycję”. Wówczas, w przypadku projektowania wyrobów o zmieniającej się geometrii (m.in. na życzenie klienta), zastosowanie przedstawionych metod zaawansowanej parametryzacji zwraca się względnie szybko (głównie z racji oszczę-dności czasu i radykalnej minimalizacji błędów projektowych), co jest właściwym uzasadnieniem podejmowania opisanych tu działań.
Niniejsze opracowanie powstało na bazie artykułu
A. Budzyński, P. Dudziak, M. Lejwoda, M. Kowalski:
W poszukiwaniu projektu idealnego, czyli przykłady przemysłowych zastosowań modelowania parametrycznego oraz optymalizacji CAD.
Artykuł ten powstał w Wyższej Szkole Gospodarki w Bydgoszczy, celem wygłoszenia podczas:
XXXV Międzynarodowe Seminarium Kół Naukowych Wydziału Mechanicznego,
Wojskowa Akademia Techniczna, Warszawa 2016.05.18-20.
Literatura:
[01] Bachan M., Bieniaszewski W., Budzyński A., Kościanowski Sz.: „Digital library of chosen injection mold standard parts, dedicated for the CAD/CAM/CAE ‘NX’ software system”, IX Międzynarodowe Seminarium Naukowe Studentów i Młodych Inżynierów Mechaników „Postępy w Inżynierii Mechanicznej”, Politechnika Gdańska Gdańsk 2006,
[02] Budzyński A., Bachan M, Urbaś Z.: „Wykorzystanie metod zaawansowanej parametryzacji MCAD osiągalnych w systemie Solid Edge na przykładzie wybranej konstrukcji”; XXVI Seminarium Kół Naukowych Mechaników, Wojskowa Akademia Techniczna Warszawa 2007,
[03] Budzyński A., Bieniaszewski W., Kościanowski Sz., Bachan M.: „Kompletna biblioteka 3D MCAD podstawowych łączników gwintowych wykonana według polskich standardów konstrukcyjnych w systemie UGS Solid Edge v18”, XXV Seminarium Kół Naukowych Mechaników, Wojskowa Akademia Techniczna Warszawa 2006,
[04] Chlebus E.: „Techniki komputerowe CAx w inżynierii produkcji”, WNT, Warszawa 2000,
[05] Dietrych J. Systemy i konstrukcje, WNT, Warszawa 1978
[06] Kazimierczak G., Pacula B., Budzyński A.: Solid Edge – komputerowe wspomaganie projektowania, Helion, Gliwice 2004,
[07] MacDonald M.: „Excel, podręcznik”, Helion, Gliwice 2005,
[08] Menchen P., Budzyński A.: „NX 8.5, ćwiczenia”, Biblioteka GM System, Wrocław 2013,
[09] Oleksiuk W. (red.): „Konstrukcja przyrządów i urządzeń precyzyjnych”, WNT, Warszawa 1996,
[10] Paprocki K.: „Zasady zapisu konstrukcji”. Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa 2006.
[11] Sydor M.: „Wprowadzenie do CAD. Podstawy komputerowo wspomaganego projektowania”. WN PWN, W-wa 2009,
[12] Walkenbach J.: “Excel 2010 PL, Formuły”, Helion, Gliwice 2011,
[13] Warneński M., Menchen P., Budzyński A.: „Modelowanie i edycja synchroniczna w Solid Edge ST”, Biblioteka GM System, Wrocław 2013.
[14] (stan na dzień 2016-03-11)
[15] https://www.se.pl/auto/ (stan na dzień 2016.03.11.)
[16] http://www.samolotypolskie.pl (stan na dzień 2016.03.11.)